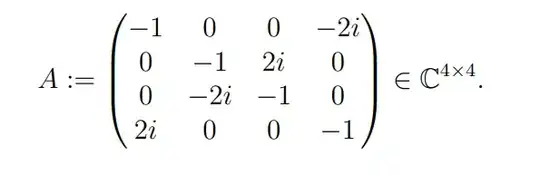1

I thought, S is self-adjoint because S^∗ = (A ^∗A) = A ^∗ (A^∗ ) ^∗ = A^∗A = S. Therefore, spectral theorem ⇒ there is an orthonormal basis {e1, ..., en} of eigenvectors of S. But I guess I'm far from the solution. I would be very happy if you have a solution suggestion or solution.

Have a good Weekends!

Question;

Over the complex numbers we consider the matrix

enter image description here

Find a unitary matrix S ∈ C ^ 4×4 such that S ∗AS is diagonal. A matrix S ∈ C^ n×n is said to be unitary if S ∗ = S¯^T = S ^−1.

A O
  • 51

1 Answers1

0

We know that every complex $n \times n$ Hermitian Matrix is unitarily diagonizable. Since A is Hermitian $(A^*=A)$ we can unitarily diagonalize it with following steps:

  1. Find Eigenvalues and corresponding Eigenvectors of A: \begin{align} &\lambda_1=1 \qquad &{}_{1}\vec{v}_1 =\begin{pmatrix}0\\i\\1\\0\end{pmatrix} \qquad &{}_{2}\vec{v}_1 =\begin{pmatrix}1\\0\\0\\i\end{pmatrix} \\\\ &\lambda_2=-3 \quad &{}_{1}\vec{v}_2 =\begin{pmatrix}0\\1\\i\\0\end{pmatrix} \qquad &{}_{2}\vec{v}_2 =\begin{pmatrix}i\\0\\0\\1\end{pmatrix} \end{align}
  2. Normalize the Eigenvectors:

\begin{align} {}_{1}\vec{w}_1 = \frac{{}_{1}\vec{v}_1}{||{}_{1}\vec{v}_1||}=\frac{1}{\sqrt{2}}\begin{pmatrix}0\\i\\1\\0\end{pmatrix} \qquad {}_{2}\vec{w}_1 = \frac{{}_{2}\vec{v}_1}{||{}_{2}\vec{v}_1||}=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\0\\0\\i\end{pmatrix} \\\\ {}_{1}\vec{w}_2 = \frac{{}_{1}\vec{v}_2}{||{}_{1}\vec{v}_2||}=\frac{1}{\sqrt{2}}\begin{pmatrix}0\\1\\i\\0\end{pmatrix} \qquad {}_{2}\vec{w}_2 = \frac{{}_{2}\vec{v}_2}{||{}_{2}\vec{v}_2||}=\frac{1}{\sqrt{2}}\begin{pmatrix}i\\0\\0\\1\end{pmatrix} \end{align}

  1. Plug the normalized vectors into a square matrix: \begin{equation} S = ({}_{1}\vec{w}_1\,\,,\,\,{}_{1}\vec{w}_2\,\,,\,\,{}_{2}\vec{w}_1\,\,,\,\,{}_{2}\vec{w}_2) = \frac{1}{\sqrt{2}}\begin{pmatrix}0&1&0&i\\i&0&1&0\\1&0&i&0\\0&i&0&1\end{pmatrix} \end{equation}
  2. Calculate the Inverse or Conjugate Transpose (easier) of $S$: \begin{equation} S^{-1}=S^{*}= \frac{1}{\sqrt{2}}\begin{pmatrix}0&-i&1&0\\1&0&0&-i\\0&1&-i&0\\-i&0&0&1\end{pmatrix} \end{equation}
  3. Check if $S^*AS$ is actually a diagonal matrix.

Note that the order of the normalized Eigenvectors in S doesn't change that S is unitary; it only changes the order of the Eigenvalues in the diagonal Matrix: \begin{align} S = ({}_{1}\vec{w}_1\,\,,\,\,{}_{1}\vec{w}_2\,\,,\,\,{}_{2}\vec{w}_1\,\,,\,\,{}_{2}\vec{w}_2)\qquad &\implies\qquad S^*AS=\text{diag}(1,1,-3,-3) \\\\ S = ({}_{2}\vec{w}_2\,\,,\,\,{}_{1}\vec{w}_2\,\,,\,\,{}_{2}\vec{w}_1\,\,,\,\,{}_{1}\vec{w}_1)\qquad &\implies\qquad S^*AS=\text{diag}(-3,1,-3,1) \\\\ S = ({}_{2}\vec{w}_2\,\,,\,\,{}_{2}\vec{w}_1\,\,,\,\,{}_{1}\vec{w}_2\,\,,\,\,{}_{1}\vec{w}_1)\qquad &\implies\qquad S^*AS=\text{diag}(-3,-3,1,1) \\\\ &\,\,\,\cdots \end{align}

Tongueofabell
  • 1