Show that $({\rm id}\otimes \Delta)\circ\Delta=(\Delta\otimes{\rm id})\circ\Delta$ "translates" to associativity of linear algebraic groups

Question

This is part of Exercise 2.1.3(1) of Springer's book, "Linear Algebraic Groups (Second Edition)". According to this Approach0 search, it is new to MSE.

Please do not use Hopf algebras.

The Question:

Check the translation

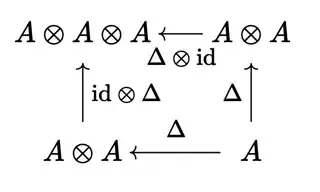
$\require{AMScd}$ $$\begin{CD}A @>\Delta>> A\otimes A\\ @V \Delta V V @VV {\rm id}\otimes\Delta V\\ A\otimes A @>>\Delta \otimes {\rm id} > A\otimes A\otimes A \end{CD}\tag{$A$}$$

of the axiom of associativity of a linear algebraic group.

(See below for notation.)

The Details:

Let $k$ be an algebraically closed field.

From pages 21 and 22 of Springer's book,

2.1.1. An algebraic group is an algebraic variety $G$ which is also a group such that the maps defining the group structure $\mu: G\times G\to G$ with $\mu(x,y)=xy$ and $i:x\mapsto x^{-1}$ are morphisms of varieties. [. . .] If the underlying variety is affine, $G$ is a linear algebraic group.

and

2.1.2. Let $G$ be a linear algebraic group and put $A=k[G]$. [. . .] [T]he morphisms $\mu$ and $i$ are defined by an algebra homomorpism $\Delta: A\to A\otimes_k A$ (called comultiplication) and an algebra isomorphism $\iota: A\to A$ (called antipode).${}^\dagger$ Moreover, the identity element is a homomorphism $e:A\to k$. Denote by $m:A\otimes A\to A$ the multiplication map (so $m(f\otimes g)=fg$) and let $\epsilon$ be the composite of $e$ and the inclusion map $k\to A$.

The group axioms are expressed by the following properties:

(associativity) the homomorphisms $\Delta \otimes {\rm id}$ and ${\rm id}\otimes \Delta$ of $A$ to $A\otimes A\otimes A$ coincide;${}^{\dagger\dagger}$

(existence of inverse) $m\circ(\iota\otimes{\rm id})\circ \Delta =m\circ({\rm id}\otimes \iota)\circ \Delta =\epsilon;$

(existence of identity element) $(e\otimes {\rm id})\circ \Delta =({\rm id}\otimes e)\circ \Delta ={\rm id}$ (we identify $k\otimes A$ and $A\otimes k$ with $A$).

The properties can also be expressed by commutative properties of the following diagrams:

$$\begin{CD}A @>\Delta>> A\otimes A\\ @V \Delta V V @VV {\rm id}\otimes\Delta V\\ A\otimes A @>>\Delta \otimes {\rm id} > A\otimes A\otimes A, \end{CD}$$

$$\begin{CD}A\otimes A @>\iota\otimes{\rm id}>> A\otimes A\\ @A \Delta AA @VV m V\\ A @>>\epsilon > A\\ @V \Delta VV @AA m A\\ A\otimes A @>> {\rm id}\otimes \iota > A\otimes A, \end{CD}$$

$$\begin{CD} A @<e\otimes{\rm id}<< A\otimes A\\ @A {\rm id}\otimes e AA {_{\rlap{\ {\rm id}}}\style{display: inline-block; transform: rotate(30deg)}{{\xleftarrow[\rule{2em}{0em}]{}}}} @AA \Delta A\\ A\otimes A @<<\Delta < A. \end{CD}$$

The full exercise is on page 22 and reads

2.1.3. Exercise. (1) Check the translation of the group axioms in 2.1.2.

Yes, that is verbatim. I am concentrating on associativity because I think, once I understand that, I'd get how to do the rest.

Thoughts:

I don't understand exactly what it is asking. What I think it means is to show that the commutative diagram $(A)$ in question implies associativity of $G$.

One thing that is clear to me is that associativity of $G$ can be described by the commutativity of the diagram

$$\begin{CD}G\times G\times G @>{\rm id}\times \mu >> G\times G\\ @V \mu\times{\rm id} V V @VV \mu V\\ G\times G @>> \mu > G. \end{CD}\tag{$B$}$$

This looks like an application of a functor, possibly $(\cdot)^*$ as defined here, would turn $(B)$ into $(A)$; I need a functor in the other direction.

---

I have included the other axioms and their respective commutative diagrams just I'm case they are needed, although I doubt they are.

---

If I knew what $\Delta$ does exactly, then I would be well upon my way to understanding the exercise.

I'm not sure what to make of ${\rm id}\otimes \Delta$ and $\Delta \otimes {\rm id}$ either.

---

$\dagger$: This is the first part of where my understanding breaks down. I think it has to do with $(\cdot)^*$ as defined here.

$\dagger\dagger$: I think this should be "$({\rm id}\otimes \Delta)\circ\Delta$ and $(\Delta\otimes{\rm id})\circ\Delta$ [. . .] coincide."

Answer 1

The key insight is that the category of affine schemes (over $k$) is the opposite of the category of (commutative) $k$-algebras. If you want to be super explicit, we have functors $\text{Spec}(-) : k\mathsf{Alg}^\text{op} \to \mathsf{Aff}_k$ and $k[-] : \mathsf{Aff}_k^\text{op} \to k\mathsf{Alg}$ which witness the equivalence.

Informally, $A = k[G]$ is a $k$-algebra, and $G = \text{Spec}(A)$ is an affine scheme over $k$.

Of course, we know that $G$ is supposed to be a group, so we have (among other things) a multiplication arrow $\mu : G \times G \to G$. We want to translate this from a condition on $G$ to a condition on $A$, so we dualize everything in sight.

Informally, the product $\times$ of affine schemes is the coproduct $\otimes$ of $k$-algebras. So our arrow of affine schemes $\mu : G \times G \to G$ is an arrow $\mu^\text{op} : A \to A \otimes A$. Similarly, the group inversion $G \to G$ dualizes to the antipode $A \to A$, and the identity $1 \to G$ (where $1$ is the terminal affine scheme) dualizes to a map $A \to k$ (where $k$ is the initial $k$-algebra). I'm sure you recognize these three arrows (in addition to the $k$-algebra structure on $A$) as the relevant structure for a hopf algebra${}^1$. This is not an accident!

If you want to be more precise with things, then we can get this result by applying the (contravariant) functor $k[-]$. As this functor is part of an equivalence between $\mathsf{Aff}_k$ and $k\mathsf{Alg}^\text{op}$ it preserves products/coproducts/etc., but products (resp. coproducts) in $k\mathsf{Alg}^\text{op}$ are coproducts (resp. products) in $k\mathsf{Alg}$. So when we apply the functor $k[-]$ to the arrow $\mu : G \times G \to G$, we find ourselves with an arrow $k[\mu] : k[G] \times k[G] \to k[G]$ in $k\mathsf{Alg}^\text{op}$. That is, an arrow $k[G] \to k[G] \otimes k[G]$ in $k\mathsf{Alg}$. Since we were writing $A = k[G]$, you'll see that this is another way of getting at the answer we computed "informally" above. Notice also that we can go backwards. If we hit this arrow $k[G] \to k[G] \otimes k[G]$ with $\text{Spec}$, then we'll get an arrow $\text{Spec}(k[G]) \times \text{Spec}(k[G]) \to \text{Spec}(k[G])$, and now we use the fact that $\text{Spec}(-)$ and $k[-]$ are parts of an equivalence to show that (up to an isomorphism in $\mathsf{Aff}_k$) this is the same thing as the arrow $G \times G \to G$ we started with!

Of course, functors also preserve commutative diagrams. So if we can express the group axioms in terms of commutative diagrams in $\mathsf{Aff}_k$ then we can find an equivalent condition, expressible in $k\mathsf{Alg}$, by hitting the relevant diagrams with $k[-]$ (or, informally, by simply reversing all the arrows).

You mentioned that you're interested in associativity in particular. So we start with a diagram in $\mathsf{Aff}_k$ expressing the associativity of $\mu$.

If we hit this with $k[-]$, and we write $A = k[G]$ and $\Delta = k[\mu]$, then we get a diagram

in $k\mathsf{Alg}$ which commutes if and only if our associativity square in $\mathsf{Aff}_k$ commutes!

Of course, I'm sure you recognize this as the co-associativity axiom for a hopf algebra. I'll leave it to you (and indeed, so did Springer) to check that the remaining axioms for $A = k[G]$ commute if and only if the relevant squares representing the group axioms commute for $G = \text{Spec}(A)$.

---

As a last aside, you mention you wish you knew what $\Delta : A \to A \otimes A$ did exactly. Obviously the exact definition will depend on your group, but you should think of $\Delta$ as "duplicating" your group element.

For instance, if $G = \mathbb{A}^1 = \text{Spec}(k[X])$ the affine line, we can compute

• $\Delta(X) = 1 \otimes X + X \otimes 1$
• $\iota(X) = -X$
• $\epsilon(X) = 0$

since each of these is also an algebra hom, they must preserve the constants in $k$, so this is enough information to define these maps on all of $k[X]$.

Then coassociativity tells us that if we apply $\Delta$ then we apply $\Delta$ again only to things on the left half of the $\otimes$, that's the same thing as applying $\Delta$ then applying $\Delta$ to the things on the right half of the $\otimes$. Explicitly:

I'll leave it to you to check that these last two terms really are equal, so that the diagram really does commute.

---

${}^1$ I know you said not to mention hopf algebras, but I feel obligated to mention these things for cultural growth. I'm not using these in any way to answer the question, so I feel justified in including it.

---

I hope this helps ^_^