How can I obtain good asymptotics for $$\gamma_n=\displaystyle\int_0^\infty\frac{t^n}{n!}e^{-e^t}dt\text{ ? }$$
[This has been already done] In particular, I would like to obtain asymptotics that show $$\sum_{n\geqslant 0}\gamma_nz^n$$
converges for every $z\in\Bbb C$.
N.B.: The above are the coefficients when expanding $$\Gamma \left( z \right) = \sum\limits_{n \geqslant 0} {\frac{{{{\left( { - 1} \right)}^n}}}{{n!}}\frac{1}{{n + z}}} + \sum\limits_{n \geqslant 0} {{\gamma _n}{z^n}} $$
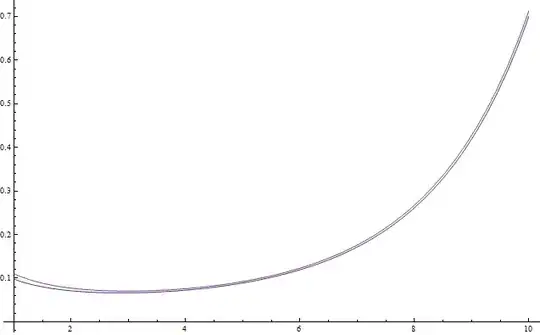
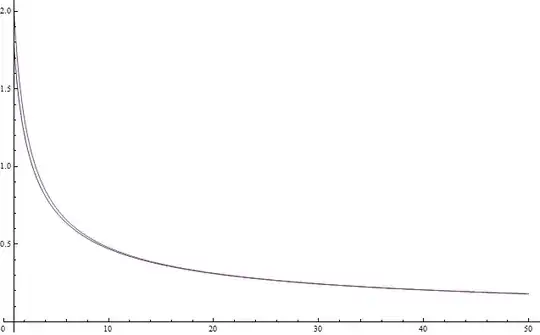
ADD Write $${c_n} = \int\limits_0^\infty {{t^n}{e^{ - {e^t}}}dt} = \int\limits_0^\infty {{e^{n\log t - {e^t}}}dt} $$
We can use something similar to Laplace's method with the expansion $${p_n}\left( x \right) = g\left( {{\rm W}\left( n \right)} \right) + g''\left( {{\rm W}\left( n \right)} \right)\frac{{{{\left( {x - {\rm W}\left( n \right)} \right)}^2}}}{2}$$
where $g(t)=n\log t-e^t$. That is, let $$\begin{cases} w_n={\rm W}(n)\\ {\alpha _n} = n\log {w_n} - {e^{{w_n}}} \\ {\beta _n} = \frac{n}{{w_n^2}} + {e^{{w_n}}} \end{cases} $$
Then we're looking at something asymptotically equal to $${C_n} = \exp {\alpha _n}\int\limits_0^\infty {\exp \left( { - {\beta _n}\frac{{{{\left( {t - {w_n}} \right)}^2}}}{2}} \right)dt} $$