Evaluation of $\int^{\infty}_{-\infty} dx \frac{x^2\cdot\exp\left(-x\right)}{\left(1+\exp\left(-x\right)\right)^2}$

Question

I can see that Wolfram Alpha can compute this, but I would like to understand how. The integrand has a poles at $\pm i\pi$ but because of the square at the bottom of the fraction, I cannot quite see how to apply residues here. The integral is also related to moments of logistic distribution https://en.wikipedia.org/wiki/Logistic_distribution (indeed this is how I got here), but cannot quite follow how the moments evaluate to results that depend on Bernoulli numbers. It would seem I am missing some transformation that would bring it into useful form. Can you please suggest how to proceed?

Thanks

Answer 1

\begin{align} \int^{\infty}_{-\infty} \frac{x^2 e^{-x}}{(1+e^{-x})^2}dx \overset{t=e^{-x}}=&\int_0^\infty\frac{\ln^2t}{(1+t)^2}dt =2 \int_0^1 \frac{\ln^2t}{(1+t)^2}dt\\ =& \ 2\int_0^1 \ln^2t \ d\left(\frac{t}{1+t}\right) \overset{ibp}=-4 \int_0^1\frac{\ln t}{1+t}dt\\ =& -4\cdot \left(-\frac{\pi^2}{12}\right)=\frac{\pi^2}3 \end{align} where $\int_0^1\frac{\ln t}{1+t}dt=-\frac{\pi^2}{12}$.

Answer 2

Integration by parts may help. Functions of the type $\int x^n f(x) \, \mathrm{d}x$ somewhat beg for it, and $\int e^{-x}\,\mathrm{d}x/(1+e^{-x})^2 $ seems easily handled.

Using the DI method to organize our work, we see that

gives us

$$\int_{-\infty} \frac{x^2 e^{-x} \, \mathrm{d}x}{(1+e^{-x})^2} = x^2 h(x) \bigg|_{-\infty}^\infty - 2x g(x) \bigg|_{-\infty}^\infty + 2 f(x) \bigg|_{-\infty}^\infty$$

where $h,g,f$ are the successive antiderivatives of $e^{-x}/(1+e^{-x})^2$.

To find $h$, firstly, I would suggest using the $u$-substitution $u=1+e^{-x}$.

To find $g$, integrate the result of the previous. Try $u=e^x$, and use partial fraction decomposition.

The antiderivative that yields $f$ is going to reference polylogarithms ($\text{Li}_2$ specifically), which have asymptotic expansions referencing Bernoulli numbers; as seen here, for $|z| \gg 1$,

$$ \operatorname{Li}_s(z) = \sum_{k=0}^\infty (-1)^k (1-2^{1-2k}) (2\pi)^{2k} {B_{2k} \over (2k)!} {[\ln(-z)]^{s-2 k} \over \Gamma(s+1-2k)} $$

and

$$\operatorname{Li}_s(z) = {\pm i\pi \over \Gamma(s)} [\ln(-z) \pm i\pi]^{s-1} - \sum_{k = 0}^\infty (-1)^k (2\pi)^{2k} {B_{2k} \over (2k)!} {[\ln(-z) \pm i\pi]^{s-2 k} \over \Gamma(s+1-2k)}$$

Apparently for non-negative integers $s$, this breaks off after finitely many terms.

Answer 3

In fact, using $$ \frac1{(1-x)^2} =\sum_{n=1}^\infty (-1)^{n-1}nx^{n-1},\int_0^\infty x^2e^{-ax}=\frac{2}{a^3}$$ one has \begin{align} &\int^{\infty}_{-\infty} \frac{x^2 e^{-x}}{(1+e^{-x})^2}dx=2\int^{\infty}_{0} \frac{x^2 e^{-x}}{(1+e^{-x})^2}dx\\ =&2\int_0^\infty \sum_{n=1}^\infty (-1)^{n-1}nx^2e^{nx}dx\\ =&2 \sum_{n=1}^\infty (-1)^{n-1}n\int_0^\infty x^2e^{nx}dx\\ =&4\sum_{n=1}^\infty (-1)^{n-1}\frac{1}{n^2}\\ =&\frac{\pi^2}3 \end{align} where $$ \sum_{n=1}^\infty (-1)^{n-1}\frac{1}{n^2}=\frac{\pi^2}{12}. $$

Answer 4

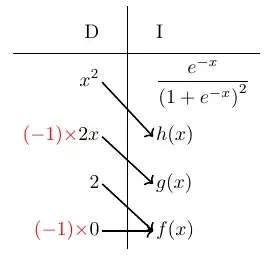
Here is an alternate and probably over-the-top method of evaluating this integral using complex analysis.

Let $I$ be the integral in question. Note that $\displaystyle \int_{-\infty}^{\infty}\frac{x^{2}e^{-x}}{\left(1+e^{-x}\right)^{2}}dx = \int_{-\infty}^{\infty}\frac{x^{2}e^{x}}{\left(1+e^{x}\right)^{2}}dx$. Let $\displaystyle f(z) = \frac{z^{3}e^{z}}{\left(1+e^{z}\right)^{2}}$. Its set of poles is $\left\{z \in \mathbb{C} : z = \pi i (2n+1)\right\}$ for all $n \in \mathbb{Z}$, but the only pole we will concern ourselves with is $z=\pi i$. Traversing counterclockwise, define a rectangular contour $C := \left\{z \in \mathbb{C} : \Re(z) \in [-R,R] \text{ } \wedge \text{ } \Im(z) \in [0,2\pi]\right\}$ visualized below.

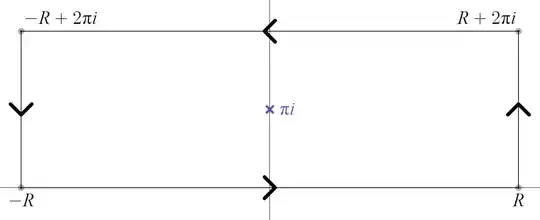
By Cauchy's Residue Theorem, we can rewrite $\displaystyle \oint_{C} f(z)dz$ as

$$2\pi i \operatorname{Res}(f(z), z = i\pi) = \left(\int_{-R}^{R}+\int_{R}^{R+2\pi i}+\int_{R+2\pi i}^{-R+2\pi i}+\int_{-R+2\pi i}^{-R}\right)f(z)dz.$$

We can prove that the integrals over the vertical line segments go to $0$ as $R \to \infty$. (I can type out a proof if someone wants me to.)

We evaluate the residue by transforming $f(z)$ as its Laurent expansion centered at its pole $z=i\pi$ like this:

$$2\pi i \operatorname{Res}\left(\frac{i\pi^{3}}{\left(z-i\pi\right)^{2}}+\frac{3\pi^{2}}{z-i\pi}-\frac{i\pi}{12}\left(36+\pi^{2}\right)-\left(1-\frac{\pi^{2}}{4}\right)\left(z-i\pi\right)+O\left(\left(z-i\pi\right)^{2}\right)\right) = 2\pi i \cdot 3\pi^2.$$

Evaluating $\displaystyle\lim_{R\to\infty}\oint_{C} f(z)dz$, we get $$ \begin{align} 2\pi i \cdot 3\pi^2 &= \lim_{R\to\infty}\left(\int_{-R}^{R}+\int_{R}^{R+2\pi i}+\int_{R+2\pi i}^{-R+2\pi i}+\int_{-R+2\pi i}^{-R}\right)f(z)dz \\ &= \lim_{R\to\infty}\int_{-R}^{R}f(z)dz + 0 + \lim_{R\to\infty}\int_{R+2\pi i}^{-R+2\pi i}f(z)dz + 0 \\ \lim_{R\to\infty}\int_{-R}^{R}f(z)dz &= 6\pi^3 i + \lim_{R\to\infty}\int_{-R+2\pi i}^{R+2\pi i}f(z)dz \\ &= 6\pi^3 i + \lim_{R\to\infty}\int_{-R}^{R}f(x+2\pi i)d(x + 2\pi i) \\ &= 6\pi^{3}i+\lim_{R\to\infty}\int_{-R}^{R}\frac{\left(x+2\pi i\right)^{3}e^{x+2\pi i}}{\left(1+e^{x+2\pi i}\right)^{2}}dx. \\ \end{align} $$

That integral on the right side is

$$\int_{-R}^{R}\frac{x^{3}e^{x}}{\left(1+e^{x}\right)^{2}}dx+6\pi i\int_{-R}^{R}\frac{x^{2}e^{x}}{\left(1+e^{x}\right)^{2}}dx-12\pi^{2}\int_{-R}^{R}\frac{xe^{x}}{\left(1+e^{x}\right)^{2}}dx-8\pi^{3}i\int_{-R}^{R}\frac{e^{x}}{\left(1+e^{x}\right)^{2}}dx.$$

The third integral above vanishes because its integrand is an odd function. Hopefully, it is trivial to prove that $\displaystyle \int_{-\infty}^{\infty}\frac{e^{x}}{\left(1+e^{x}\right)^{2}}dx = 1$.

Going back to $\displaystyle\lim_{R\to\infty}\oint_{C} f(z)dz$, we get

$$ \begin{align} \lim_{R\to\infty}\int_{-R}^{R}f(z)dz &= 6\pi^3 i + \lim_{R\to\infty}\int_{-R}^{R}f(x)dx + 6\pi i I - 12\pi^2 (0) - 8\pi^3 i (1). \\ \end{align} $$

In conclusion, the integral $I$ is $\displaystyle \frac{\pi^2}{3}$, and we are finished!