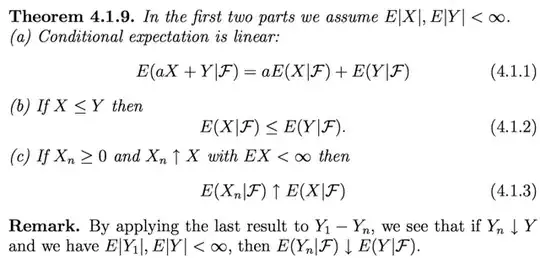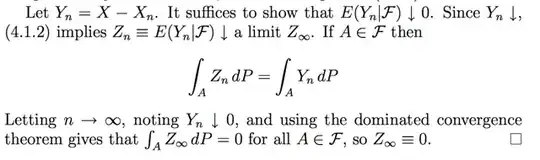2

The theorem below is from Durret's Probability Theory and Example. I am struggling to follow the proof of (c). I will try to give all my thought here. By the definition of conditional expectation and (b), we have for all $A\in \mathcal{F}$ $$ \int_A X_n dP = \int_A E(X_n|\mathcal{F})dP\leq \int E(X|\mathcal{F})dP=\int_A XdP $$ So by the squeeze theorem, $\int_A E(X_n|\mathcal{F})dP\rightarrow \int_A E(X|\mathcal{F})dP$. The tricky part is then to show this implies $ E(X_n|\mathcal{F}\rightarrow E(X|\mathcal{F})$ almost surely.

Durret's approach seems to use dominated convergence theorem and this property of integral (link to another SE question). However, I don't exactly follow his steps. Why does $Y_n\downarrow 0\implies Z_\infty$ exists? What is the random variable with finite expectation that bounds $Z_n$ (in order to use DCT)? I guess $Y_1$ works beause $E(Y_1)=E(X)-E(X_1)<\infty$ where $0\leq E(X_1\leq E(X)<\infty$.

A longer proof would be most welcome (or explain all four steps in the proof).

enter image description here

Proof:

enter image description here

enter image description here

chuck
  • 701
  • 1
    Bounded monotone sequences have a limit + the limit of measurable functions is a measurable function – Snoop Mar 26 '23 at 21:45
  • @Snoop But the sequence is decreasing so MCT doesn't apply right? – chuck Mar 26 '23 at 22:14
  • 1
    No it is not right. It obviously applies. – Snoop Mar 26 '23 at 23:00
  • @Snoop Thanks for the correction. I got confused as Durret defined $Z_\infty$ to be the lim sup rather than lim inf, which is also correct. – chuck Mar 26 '23 at 23:54
  • @Snoop Btw, would you give me reference to this theorem where bounded monotone sequences of random variable have a limit? – chuck Mar 27 '23 at 00:11
  • That is not what I said. Please refer to my answer and let me know. – Snoop Mar 27 '23 at 10:12

1 Answers1

1

Please let me know if the following is not clear. All equalities and inequalities of conditional expectations hold a.s. Now consider $(Z_n)_{n \in \mathbb{N}}$ which are versions of the conditional expectations $E[Y_n|\mathscr{F}]$ and some $$\omega \in \bigcap_{n \in \mathbb{N}}\{Z_n=E[Y_n|\mathscr{F}]\}\cap \{E[Y_{n+1}|\mathscr{F}]\leq E[Y_{n}|\mathscr{F}]\}\cap \{E[Y_n|\mathscr{F}]\geq 0\}$$ This implies $0\leq ...\leq Z_{n+1}(\omega)\leq Z_{n}(\omega)\leq ...\leq Z_1(\omega)$. Since the sequence $(Z_n(\omega))_{n \in \mathbb{N}}$ is monotone decreasing and bounded below by $0$, it has a limit $\lim_nZ_n(\omega)=\inf_nZ_n(\omega)$. Now, also note $Z:=\inf_nZ_n$ is a measurable function. So we conclude that $\omega \in \{Z_n\to Z\}$; since $\omega$ was arbitrary, we have the set inclusion and $$P(Z_n\not\to Z)\leq \sum_{n \in \mathbb{N}}(P(Z_n\neq E[Y_n|\mathscr{F}])+P(E[Y_{n+1}|\mathscr{F}]> E[Y_{n}|\mathscr{F}])+P(E[Y_n|\mathscr{F}]< 0))=0$$ since the sets we are measuring on the rhs of the inequality have probability zero. So $Z_n \to Z$ a.s. By definition, we also have that $0\leq Z_n\leq Z_1,\,\forall n$ a.s. so we can apply DCT.

Snoop
  • 15,214
  • Could you clarify what $\omega \in {Z_n\to Z}$ and $P(Z_n\not\to Z)$ mean? – chuck Mar 27 '23 at 16:09
  • 1
    @chuck the set ${Z_n\to Z}$ is the set of $\omega$ s.t. $Z_n(\omega)$ converges to $Z(\omega)$. The set ${Z_n\not\to Z}$ is the complement of such set: ${Z_n\not\to Z}={Z_n\to Z}^c$. – Snoop Mar 27 '23 at 16:13