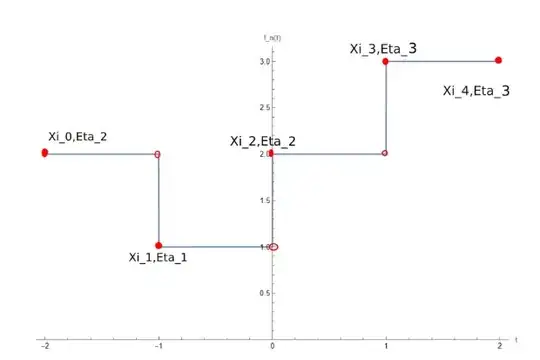
I have the following plot:
which is reflected by the given formula:
$$ \chi_{A_j}(\xi)=\begin{cases} 2, \ \ \ \ -2\le \xi<-1 \\ 1, \ \ \ \ -1\le \xi<0 \\ 2, \ \ \ \ 0\le \xi<1 \\ 3, \ \ \ \ 1\le \xi\le2 \end{cases} $$
However, when I try to write this formula in the form of:
\begin{equation} f(\xi):=\sum_{j=1}^n \eta_j\chi_{A_j}(\xi), \ \ \ \ \ \ \ \end{equation} where $j=1,2,3,4,5$ and $A_{j}$=$[\xi_{j-1}, \xi_{j}]$ and $\eta_j=[\eta_1,\eta_2,\eta_3]=[1,2,3]$
I get problems. $\eta_j$ in the sum formula does not correspond to $\eta_j$ in the plot.
How can I write the sum formula so that it reflects this function correctly?
Any ideas appreciated!
Thanks