1

I'm trying to get the "volume" weighted mean of grades for students in 3 classes. There are 4 students in total and the below shows each student's grade.

A = {100}

B = {200}

C = {310, 290}

The mean grade for each class is:

A = 100

B = 200

C = (310+290)/2 = 300

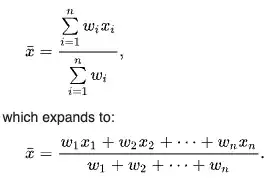
Finally, I'm calculating the weighted mean of grades for all students in 3 classes: enter image description here

$$ \frac{(1 \times 100) + (1 \times 200) + (2 \times 300)}{1 + 1 + 2} = 225 $$

However, I'm not sure if I'm truly calculating "weighted" mean of grades for all students, as the simple arithmetic mean of grades also gives the same result:

$$ \sum_{i=1}^n \frac{Grades}{num. of students} = \frac{100+200+310+290}{4} = 225 $$

Is there something wrong with my logic, calculation, and/or dataset?

user9532692
  • 145
  • Perhaps rewrite the question replacing the vague business jargon and database-style labels with natural language and nicer variables; not only does this make for more pleasant reading, more importantly it helps clarify your own thinking/analysis. As you're basically developing definitions, I believe that precision and simplicity are important and helpful. P.S. In mathjax, write \times instead of *. – ryang May 18 '23 at 04:09
  • 1
    Hi ryang, I tried to simplify the problem by using a different example and removing business jargons. Hope this helps clarify my question. Thanks in advance for your feedback :) – user9532692 May 18 '23 at 05:27

2 Answers2

1

Yes, these two quantities, the "weighted mean of the mean" and "overall mean", are always equal. Suppose there are $k$ classes and let the $i$th classes have $n_i$ students, with sum of grades $s_i$. Then the mean grade for the $i$th class is $s_i/n_i$. The overall total grade is $s_1 + s_2 + \dots + s_k$ and the total number of students is $n_1 + n_2 + \dots + n_k$. So the two quantities are: $$\frac{n_1 (\frac{s_1}{n_1}) + n_2 (\frac{s_2}{n_2}) + \dots + n_k(\frac{s_k}{n_k})}{n_1 + n_2 + \dots + n_k}$$ and $$\frac{s_1 + s_2 + \dots + s_k}{n_1 + n_2 + \dots + n_k},$$ and it should be clear that these are equal.

ronno
  • 11,390
1

Yes, the whole point of computing the average of the class averages using the class sizes as weights is to obtain the "overall average" (i.e., the average score of the student body)!

Say the average score of class A (2 students) is 43 while the average score of class B (30 students) is 87; which score do you think is closer to the overall average?

Giving class B greater weightage is precisely the adjustment we are making to obtain 84.25 marks (the weighted average of the two averages) instead of 65 marks (the simple average of the two averages).

It’s worth being extra precise/systematic as you are sorting this out! In your example, what you call the "weighted average score of all the students" (I'm paraphrasing for simplicity) is actually instead a weighted average of the three class averages (each datum is some average score, not some individual score); but as has turned out, this is simply the average score—the adjective 'weighted' not necessary—of all the students. $\quad$ And while you are referring to the overall average as some simple arithmetic average, do remember that the average, 200, of the three class averages, is also a simple arithmetic average.

The point is that when dealing with your data set, there is not just one single weighted average (what are you assigning as weights?), and there is not just one single simple average (average of what precisely?).

(And as you know, average can also refer to median, geometric mean, etc.)

ryang
  • 38,879
  • 14
  • 81
  • 179
  • So your example of obtaining 84.25 as the average of the class averages using the class sizes as weights is the same as how I'm calculating the averages using class sizes as weights (225), am I right? – user9532692 May 18 '23 at 17:08
  • 1
    @user9532692 Yeap; I created that more extreme/hyperbolic example to throw into sharper relief the mechanics of weighted averaging. Your example was so timid. -) – ryang May 18 '23 at 17:28