There are various ways to try this. My own "non-rigorous" way would be like this :
We have Constant Answer which is not Dependant on $g(x)$ , as long as that Integral is $3$.
(1) Let $g(x)=Constant=3/2$ , then $\int_{-1}^{+1}g(x)dx=3x/2|_{-1}^{+1}=3/2+3/2=3$.
Then we have $f(x,y,z)=g(x+y+z)=3/2$
Then we have $\int\int\int_{V}f(x,y,z)dxdydz=\int\int\int_{V}g(x+y+z)dxdydz=\int\int\int_{V}(3/2)dxdydz=(3/2)|_{V}=3V/2$
The Volume $V$ is a "Diamond" in 3D , where the Diagonals are the 3 Axis , between $-1$ & $+1$ , in other words , Diagonal length is $2$. Hence Cube Side "Diamond" Side is $\sqrt{2}$.
Image :
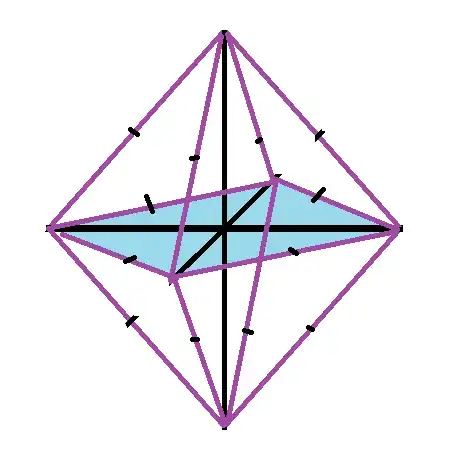
Purple lines are Equal Sides of the "Diamond" , Black lines are Equal Diagonals.
The "Diamond" is made of 2 Pyramids , each with height $2$ & Square Base with Side $\sqrt{2}$.
Blue Area is the Square Base of the Pyramids.
https://www.varsitytutors.com/hotmath/hotmath_help/topics/volume-of-a-pyramid : "volume of a pyramid = one-third the area of the base times the height" : $\sqrt{2}\times\sqrt{2}\times{2}/3=4/3$
Volume Of Our "Diamond" made of 2 Pyramids is $V=2\times(4/3)=8/3$
Hence the Volume $V$ is $8/3$ which is the Integral Domain we want.
That then gives Integral Value $(3/2)V=(3/2)(8/3)=4$
(2) We can take $g(x)=9x^2/2$ , then $\int_{-1}^{+1}g(x)dx=9x^3/6|_{-1}^{+1}=3/2+3/2=3$.
Integrating $f(x,y,z)=9(x+y+z)^2/2$ thrice & using the limits will be a little Cumber-Some , yet , we know that we have to get the Same Answer $4$.
