Since we have the angle and the radii we do indeed have $BC$. Here is my solution:
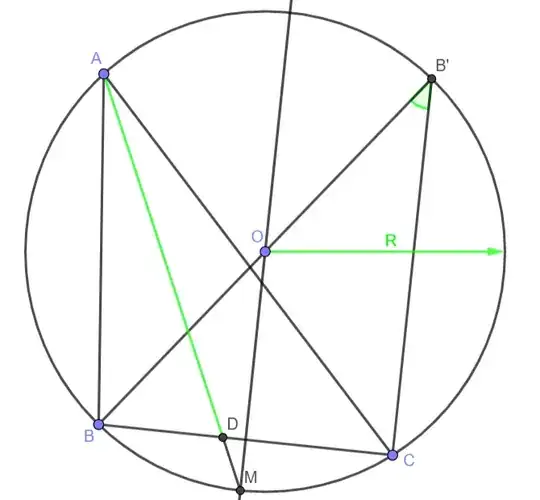
Let's begin with a random point $O$ of the plane to be the center of our circle $\omega = \odot (O,R)$ whose radius $R$ is given to us. Now take a random point $B$ on the circumference of $\omega$ and let $B' = BO \cap \omega \neq B$, then draw line $B'C$ ($C \in \omega$) such that $\angle BB'C = \angle A$ be the given angle we want to have on vertex $A$.
Let $M$ be the meeting of the perpendicular bissector of $BC$ with $\omega$ on the arc $\widehat{BC}$ that doesn't contain $B'$.
Now suppose we have found our solution i.e. the point $A$, let $D = AM \cap BC$. There is a famous result on geometry called the shooting lemma, which states that $MD \cdot MA = MC^2 = MB^2$.
We want $MD = x$, we have $MC = b$ and $AD = a$. All we need is to geometrically solve the equation $x \cdot (x+a) = b^2$. Although I lack a good solution, here is a bad one using a basic concept of power of a point:
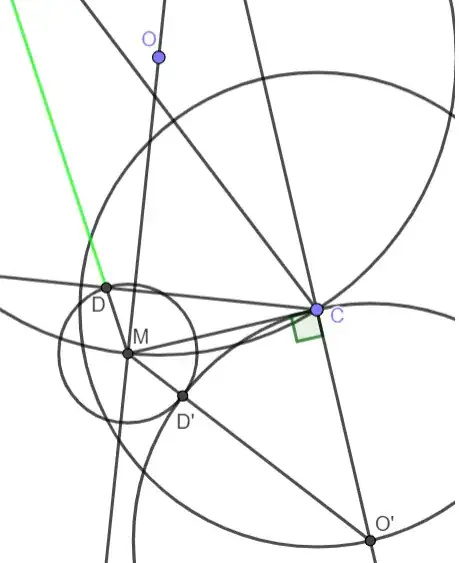
- Draw line $CO' \perp MC$
- Draw circle $c_1 = \odot(C, \frac{AD}2)$
- Let $O' = c_1 \cap CO'$ and draw circle $c_2 = \odot (O',O'C)$
- Let line $MO'$ meet $c_2$ at point $D'$ closer to $M$ than to $O'$
- $D = \odot (M,MD') \cap BC$ (there are usually two solutions)
- $A = MD \cap \omega \neq M$


