Maximum and Minimum of $\displaystyle \frac{36}{a}+\frac{25}{b}$

Question

If $\displaystyle \frac{a^2}{36}-\frac{b^2}{25}=1$.Then range of $\displaystyle \frac{36}{a}+\frac{25}{b}$ is

Using Trigonometric Substution, We have

$\displaystyle a=6\sec\theta$ and $y=5\tan\theta$.

Then we have expression

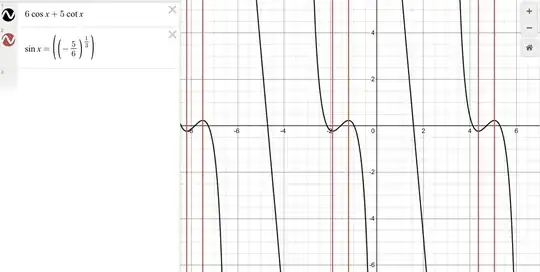
$\displaystyle f(\theta)=6\cos\theta+5\cot\theta$

Then we have $\displaystyle f'(\theta)=-6\sin\theta-5\csc^2\theta$

Now for maximum and minimum , We have $\displaystyle f'(\theta)=0$

$\displaystyle 6\sin\theta+5\csc^2\theta=0\Longrightarrow \sin\theta=-(5/6)^{\frac{1}{3}}$

And $\displaystyle f''(\theta)=-6\cos\theta+10\csc^2\theta\cot\theta$

Put $\displaystyle \sin\theta=-(5/6)^{\frac{1}{3}}$ in $f''(\theta)$

Please have a look on that problem

Answer 1

Let $x=\frac{a}{6}, y=\frac{b}{5}$. Then, the condition becomes $x^2-y^2=1$ and we want to find the range of $\frac{6}{x}+\frac{5}{y}$.

Notice we can let $x$ approach $1$. Then, $y$ will also approach $0$. If we let $y$ be negative, then $\frac{6}{x}+\frac{5}{y}$ will blow up to $-\infty$. If we let $y$ be positive, then $\frac{6}{x}+\frac{5}{y}$ will blow up to $+\infty$.

Hence, the range of $\frac{6}{x}+\frac{5}{y}$ is $(-\infty, +\infty)$.

Answer 2

Since $\;\dfrac{a^2}{36}-\dfrac{b^2}{25}=1\,,\,$ it follows that $\;a=\pm\dfrac65\sqrt{b^2+25}\;.$

Moreover ,

$\dfrac{36}a+\dfrac{25}b=\pm\dfrac{30}{\sqrt{b^2+25}}+\dfrac{25}b\;.$

Now we consider the function $\;f:(-\infty,+\infty)\setminus\{0\}\to\Bbb R\;$ which is defined as follows :

$f(b)=\dfrac{30}{\sqrt{b^2+25}}+\dfrac{25}b\quad$ for any $\;b\in(-\infty,+\infty)\setminus\{0\}\,.$

Since $\,\lim_\limits{b\to+\infty}f(b)=0^+,\,$ $\lim_\limits{b\to0^+}f(b)=+\infty\,$ and the function $\,f(b)\,$ is continuous on $\,(0,+\infty)\,,\,$ by applying the intermediate value theorem, it follows that

$\mathrm{range}\left(\dfrac{36}a+\dfrac{25}b\right)\supseteq\mathrm{range}\big(f(b)\big)\supseteq(0,+\infty)\,.\quad\color{blue}{(1)}$

Furthermore, since

$f(-10)=\dfrac{30}{\sqrt{125}}-\dfrac{25}{10}>\dfrac{30}{\sqrt{144}}-\dfrac{25}{10}=\dfrac{30}{12}-\dfrac52=0\;,$

$\lim\limits_{b\to0^-}f(b)=-\infty\,$ and the function $\,f(b)\,$ is continuous on $\,[-10,0)\,,\,$ by applying the intermediate value theorem, it follows that

$\mathrm{range}\left(\dfrac{36}a+\dfrac{25}b\right)\supseteq\mathrm{range}\big(f(b)\big)\supseteq(-\infty,0]\,.\quad\color{blue}{(2)}$

From $\,(1)\,$ and $\,(2)\,,\,$ it follows that

$\mathrm{range}\left(\dfrac{36}a+\dfrac{25}b\right)=(-\infty,+\infty)\,.$

Answer 3

As $f(x) = 6 \cos x + 5 \cot x$ it will be a kind of asymptotic function and you can’t simply check for global maxima and minima by its derivative as it will give you the point of zero slope which is not true for the true maxima which will be a asymptote.

Answer 4

The equation: [(a2 / 36) – (b2 / 25)] = 1 represents a hyperbola which passes through (6,0) and (-6,0)

The value of 36 / a + 25 / b approaches +∞ and -∞ from upper hand limit and lower hand limit respectively at these points

Hence range is (-∞,+∞).

Answer 5

I'm not sure how to proceed with the trigonometric analysis, but the answer to your question is $\infty$ and $-\infty$.

Minimum = $-$ Maximum, since if $(a,b)$ satisfies the constraint, then $(-a,-b)$ will also satisfy. $a=6, b=0$ satisfies the constraint, and that blows your function up to $\infty$.

If you were to restrict $a,b\geq0$, then minimum would be $0$ instead, as you can make $a,b$ very large