Does $\sum\limits_{k=1}^n\dfrac{1}{k^{1+|\sin k|}}$ approach $a\ln (\ln n)$?

Question

$\sum\limits_{k=1}^{\infty}\dfrac{1}{k^{1+|\sin k|}}$ has been shown to diverge. This made me wonder about the asymptotics of $S(n)=\sum\limits_{k=1}^n\dfrac{1}{k^{1+|\sin k|}}$.

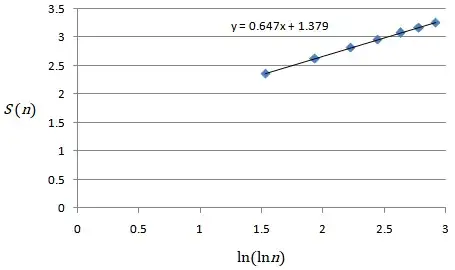
Numerical investigation suggests that $S(n)$ against $\ln (\ln n)$ may have a linear asymptote:

Does $L=\lim\limits_{n\to\infty}\dfrac{\sum\limits_{k=1}^n {k^{-(1+|\sin k|)}}}{\ln (\ln n)}$ equal a positive real number, and if so, does it have a closed form?

Not quite an answer because the details aren't quite right but it seems like it might not just be a "fluke at small values" if you look at this answer (it's with $\cos$ instead of $\sin$ but it shouldn't matter much): Convergence/Divergence of infinite series $\sum\limits_{n=1}^{\infty} \frac{1}{n^{1+\left|{\cos n}\right|}}$. The reason this is good is that you can then look at the ("simpler") asymptotic expansion of $\sum_{k = 1}^n \frac{1}{k\ln(k)}$, and it is in fact of the type $\mathrm{constant} + \ln(\ln(n)) + \mathrm{other,terms}$: (1/2) — Bruno B, Jul 22 '23 at 13:02
You can see the beginning of the expansion in this Maple excerpt: https://les-mathematiques.net/vanilla/index.php?p=/discussion/comment/389785/#Comment_389785 (2/2) — Bruno B, Jul 22 '23 at 13:04
Exen if the regression shows a very large $R^2$, have a look at the distribution of the residuals. — Claude Leibovici, Jul 23 '23 at 02:52

Does $\sum\limits_{k=1}^n\dfrac{1}{k^{1+|\sin k|}}$ approach $a\ln (\ln n)$?

0 Answers0