12

I'm reading through Aluffi's Algebra Chapter 0 and one of the exercises is to come up with a definition of an epimorphism and show that a map $f \colon A \to B$ is surjective iff it is an epimorphism.

In hindsight it's obvious to say that (Definition 1) $f$ is an epimorphism if for all maps $g_1, g_2 \colon B \to Z$, if $g_1 \circ f = g_2 \circ f$, then $g_1 = g_2$ (right-cancellation).

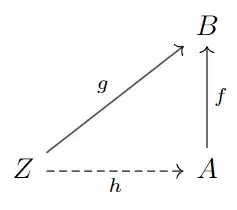
However, when I first approached the problem I had something about existence in mind and I came up with the following diagram:

Commutative diagram

Here, I wanted to define an epimorphism as follows: (Definition 2) $f$ is an epimorphism if for all maps $g \colon Z \to B$, there exists a map $h \colon Z \to A$ such that $g = f \circ h$.

In that case, a proof would go as follows (I will assume all sets $A,B,Z$ are nonempty):

Suppose $f$ is surjective. Then, for all $b \in B$, the preimage $f^{-1}(\{b\})$ is nonempty, so we can pick an element $a_b \in A$ such that $a_b \overset{f}{\mapsto} b$. Now if $z \overset{g}{\mapsto} b$ for $z \in Z$, then we can let $h(z)=a_b$. We can repeat this exercise for any $b' \in B$ that is mapped to under $g$.

On the other hand, suppose $f$ is an epimorphism according to Definition 2. Choose an element $b \in B$ and let $g$ be the constant map $g(z) \equiv b$. Then there exists a map $h \colon Z \to A$ such that $f(h(z))=g(z)=b$, so there is some $a \in A$ mapping to $b \in B$ under $f$. Again we can repeat this for any $b' \in B$.

Question 1 Is my proof correct and the definition sound?

Question 2 If the answer to Q1 is yes, then I assume I didn't just invent some new property in category theory but rather that this is some property that possibly has a name. (Would it qualify as a universal property?)

HallaSurvivor
  • 38,115
  • 4
  • 46
  • 87
user2978125
  • 349
  • 3
    Note that in some concrete categories we find epis which are not surjective maps. A simple example is the category of topological spaces, where the inclusion $\mathbb Q \to \mathbb R$ is epic (satisfies def.1) but not surjective (and violates def. 2). Bonus: it is also monic (since it's injective), but not an isomorphism. – chi Jul 24 '23 at 15:17
  • 3
    A more algebraic standard example of what @chi points out: The inclusion $\mathbb Z \rightarrow \mathbb Q$ is an epimorphism in the category of commutative rings. Obviously it is not surjective. – Torsten Schoeneberg Jul 24 '23 at 17:10
  • Thanks, this adds some good context as to why 'epimorphism' isn't just another term for 'surjective' or 'onto'. – user2978125 Jul 25 '23 at 14:34
  • 1
    Errata to my comment above: the inclusion $\mathbb Q \to \mathbb R$ is epic in the category of Hausdorff topological spaces, since there a function $\mathbb R \to X$ is uniquely determined by its behavior on rationals. See this question for more discussion, and a proof that in the category of all topological spaces all epis are in fact surjective. – chi Jul 25 '23 at 15:26

3 Answers3

18

Your definition doesn't work in general, basically because of algebraic obstructions.

For instance, imagine $f : \mathbb{Z} \to \mathbb{Z}/2$ is the usual "reduce mod $2$" map in the category of groups. Then taking $g : \mathbb{Z}/2 \to \mathbb{Z}/2$ to be the identity map, we have a picture like yours, but notice there is no map $h : \mathbb{Z}/2 \to \mathbb{Z}$ making the diagram commute. In fact, the only group homomorphism $\mathbb{Z}/2 \to \mathbb{Z}$ is the trivial homomorphism. I'll let you explicitly work through why your proof doesn't work on this example, because I think it will be a good exercise ^_^.

However, you're not far off from a very useful criterion! We say that $Z$ is a projective object in a category if for every epimorphism $f : A \twoheadrightarrow B$ and every map $g : Z \to B$, we have a lift $h : Z \to A$ making the triangle commute. Notice this is a condition on $Z$, rather than a condition on $f$! In $\mathsf{Set}$, every object is projective (this is equivalent to the axiom of choice) so we can always detect epimorphisms by checking if a lift exists! Unwinding the fancy words gives basically the same proof that you gave (which does work in the category of sets), but it fails in other categories because of the lack of projectives.

I hope this helps ^_^

HallaSurvivor
  • 38,115
  • 4
  • 46
  • 87
  • 2
    Thank you, I think I see it! In my proof I tacitly assumed $h$ is just a function, but if we talk about groups, I would also have to check that $h$ is a group homomorphism (not just some arbitrary map). In your example with $\mathbb{Z}/2$ and $\mathbb{Z}$, we would need $h$ to be the inclusion map, but then $h(1+{\mathbb{Z}/2}1) = h(0) = 0 \neq 2= h(1)+{\mathbb{Z}}h(1)$. The lifting criterion for projective objects is interesting (sorry if this is not the correct terminology)! – user2978125 Jul 24 '23 at 15:08
  • @user2978125 -- That's it exactly! ^_^ – HallaSurvivor Jul 24 '23 at 16:51
  • Also, if you keep going with Aluffi's book, you'll meet projectives objects again in "Linear Algebra, Reprise" – HallaSurvivor Jul 24 '23 at 16:54
  • Perfect, thank you! (+1 for good exercise) – user2978125 Jul 24 '23 at 20:11
11

Question 1 Is my proof correct and the definition sound?

Yes, though the proof that surjective maps have this property uses the axiom of choice, which is fine.

Question 2 If the answer to Q1 is yes, then I assume I didn't just invent some new property in category theory but rather that this is some property that possibly has a name. (Would it qualify as a universal property?)

This is equivalent to the map being a split epimorphism. A morphism $f : A \to B$ is a split epimorphism if there exists a map $g : B \to A$ such that $f \circ g = \mathrm{id}_B$. That is, $f$ must have a right inverse.

Assume $f$ has your property. Then applying it with $g = \mathrm{id}_B$, the $h$ in your property is a right inverse to $f$.

Conversely, suppose that $f$ is a split epimorphism with right inverse $f^\dagger$. Then for any $g : Z \to B$, define $h : Z \to A$ by $f^\dagger \circ g$. Then $f \circ h = f \circ f^\dagger \circ g = \mathrm{id}_B \circ g = g$.

S.C.
  • 2,630
3

I'd like to add a higher view on the problem. Consider these four definitions given a morphism $f : A \to B$

  • The map $\hom(C,A) \to \hom(C,B)$ induced by composition is injective for all $C$.
  • The map $\hom(C,A) \to \hom(C,B)$ induced by composition is surjective for all $C$.
  • The map $\hom(B,C) \to \hom(A,C)$ induced by composition is injective for all $C$.
  • The map $\hom(B,C) \to \hom(A,C)$ induced by composition is surjective for all $C$.

It's easy to see that the standard definition of monomorphism is just the first one, but epimorphism the third one. And your purposed definition is the second one. These four are called mono, split epi, epi, split mono, respectively. The first and third are the appropriate duals, since being mono in $\mathcal C^{\mathsf{op}}$ is exactly the same as being epi in $\mathcal C$. Thus we give similar names to them. The second and fourth are also duals.

(Also, since this is in a presheaf category, being injective/surjective at each object is equivalent to being mono/epi as presheaves.)

Trebor
  • 4,575