The imaginary golden ratio is given by
$$\varphi_i = \frac{1+\sqrt{3}i}{2}=e^{i\pi/3}$$
This has many properties in common with the golden ratio and has been adequately described here (Imaginary Golden Ratio) and here.
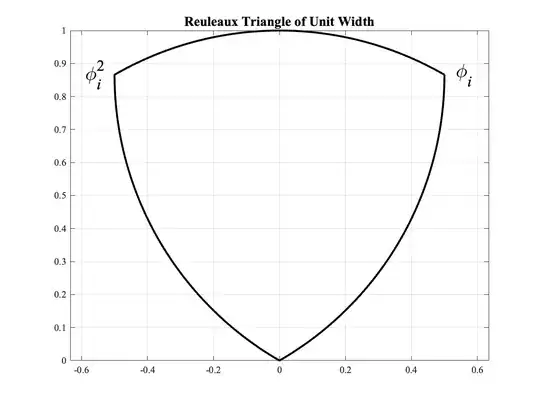
If we look at the normalized Reuleaux triangle (i.e., of unit width) as in the figure below, we’ll see that the corners are given by $\varphi_i,\ \varphi_i^2,\ \varphi_i^2-\varphi_i+1=0$. It’s also worth noting that the centroid is given by the average of these three points, to wit, $z_c=i/\sqrt{3}$.
I have looked for equations for the Reuleaux triangle, but have found only one that was given by Jan M, reproduced here, albeit in complex form
$$z=2\cos(\pi/2n)\cdot \exp\bigg(\frac{i}{2}\bigg(t+\frac{\pi}{n}\big(2\lfloor nt/2\pi\rfloor+1\big)\bigg)\biggr)- \exp\biggr(\frac{i\pi}{n}\big(2\lfloor nt/2\pi\rfloor+1\big)\bigg)$$
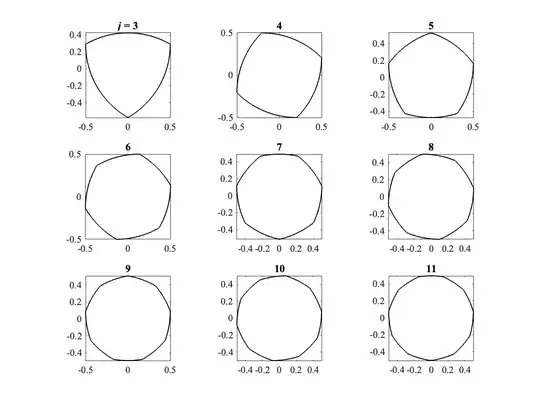
This is an equation for all the Reuleaux polygons ($n\ge3,\ n \text{ odd}$). This equation works for even $n$ as well, but these polygons do not satisfy the Reuleaux requirement of uniform width. There is nothing (that I can see, at least) that gives any hint of the imaginary golden ratio.
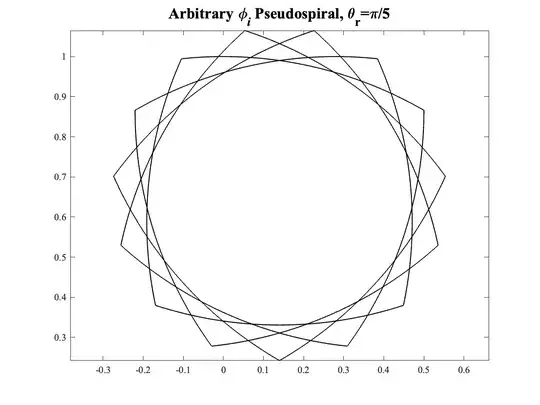
In the answer that follows, I will demonstrate the Reuleaux triangle, indeed, all the Reuleaux polygons, as degenerate pseudospirals, with known analytic solutions.