Answer with no trigonometry... Let $\triangle ABC$ be isosceles with $AB=AC$. Let $D$ such that $BD=AD$. Calculate the angles of the triangle $AED$.

Question

PROBLEM

Let $\triangle ABC$ be isosceles with $AB=AC$. On the extension of side $BC$, a point $D$ is considered such that $C$ belongs to side $BD$ and $BD=AD$. If the bisector $\angle ACD$ forms with the side $AB$ an $\angle AEC$ with a measure of $30$, calculate the measures of the angles of the triangle $AED$.

WHAT I THOUGHT OF

First of all, the drawing:

Ok, so as you can see I noted $\angle BAC=x$ and $\angle CAD=y$

Using the fact that $AB=AC$ and $BD=AD$ we can simply show that $30=\frac{y}{2}$ $=>$ $y=60$, $x=20$

We found out that $\angle EAD=80$.

Now, I don't know how to calculate the other angles.

I thought of using the intern bisector or extern bisector theorem or Ceva's theorem, but it didn't send me any useful ideas. Hope one of you can help me!

Answer 1

Proceeding from the point you stopped by, let's assume $\angle MED=\alpha.$ Then, $\angle MDE=70^{\circ}-\alpha$.

By the law of sines in $\triangle AED$, we have:

$$\frac{\sin \alpha }{\sin 30^{\circ}}=\frac{DM}{AM}\times \frac{AE}{ED}.$$

But, since the segment $CX$ is the bisector, we get that: $\frac{DM}{AM}=\frac{DC}{AC}.$

Hence,

$$\frac{\sin \alpha }{\sin 30^{\circ}}=\frac{DC}{AC} \times \frac{AE}{ED} \\= \frac{\sin 60^{\circ}}{\sin 20^{\circ}}\times \frac{\sin (70^{\circ}-\alpha)}{\sin 80^{\circ}}= \frac{\sin 60^{\circ}}{\sin 20^{\circ}}\times \frac{\cos (20^{\circ}+\alpha)}{\sin 80^{\circ}}.$$

On the other hand, $\sin 20^{\circ}\sin 40^{\circ}\sin 80^{\circ}=\frac{\sqrt 3}{8}$ (look at this ), so:

$$\frac{\sin \alpha}{\cos (20^{\circ}+\alpha)}=\frac{\sin 40^{\circ}}{\cos 60^{\circ}}=\frac{\sin 40^{\circ}}{\cos (20+40)^{\circ}} \implies \alpha=40^{\circ}.$$

Answer 2

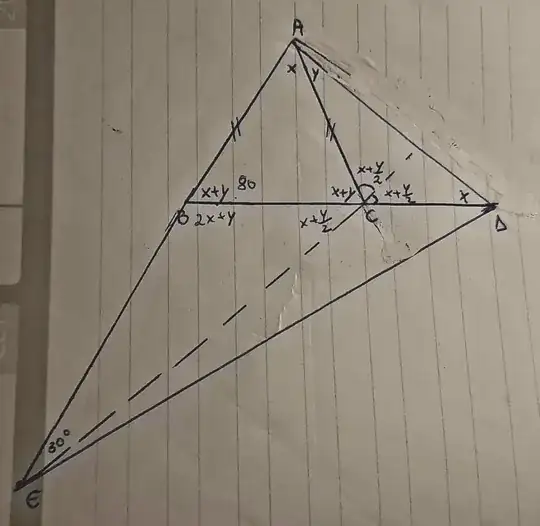
I'm going to start with the information you were already able to find. Let $F$ be the intersection between the bisector of $A\hat{C}D$ and side $AD$; let $H$ be a point in $BD$ such that $H\hat{A}D = B\hat{A}C = 20^{\circ}$; and let $J$ be the intersection between $AH$ and $CF$.

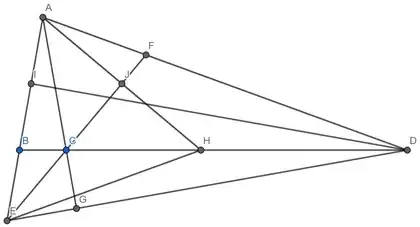
Solution 1 (using isogonal conjugate):

$\triangle ADH$ is isosceles and $\overline{AH} = \overline{DH}$. Now, in triangle $\triangle ACH$, we have $C\hat{A}H = 40^{\circ}$, and since $A\hat{H}D = 140^{\circ}$, we have $A\hat{H}C = 40^{\circ}$ and so $\triangle ACH$ is isosceles, which means the bisector $CJ$ is also the altitude and $C\hat{J}H = E\hat{J}H = 90^{\circ}$.

Note that, since $CJ$ is the altitude of the isosceles triangle, it is also the median and $\overline{AJ} = \overline{HJ}$. But then triangles $\triangle AEJ$ and $\triangle EJH$ are congruent (SAS congruence) and so $\overline{EH} = \overline{AE}$. But note that $E\hat{A}H = 60^{\circ}$ and $A\hat{E}H = 30^{\circ} + 30^{\circ} = 60^{\circ}$, so $\triangle AEH$ is equilateral and $\overline{EH} = \overline{AH} = \overline{DH}$, which means $H$ is the circumcenter of $\triangle AED$. Since the circumcenter is the isogonal conjugate of the orthocenter and $AH$ and $AG$ are isogonal conjugates, then $AG$ is the altitude of $\triangle AED$, thus $A\hat{G}E = 90^{\circ}$, so clearly $A\hat{E}G = 70^{\circ}$ and then you can find all other angles from here.

Solution 2 (without isogonal conjugate):

Note that since $C\hat{A}D = 60^{\circ}$ and $A\hat{D}C = 20^{\circ}$, then $A\hat{C}D = 100^{\circ}$ and so $J\hat{H}C = 50^{\circ}$. We know $H\hat{E}C = 30^{\circ}$ (explained in solution 1) and since $J\hat{H}C = 50^{\circ}$, then $E\hat{C}H = 130^{\circ}$. By the external angle theorem $E\hat{H}D = H\hat{E}C + E\hat{C}H = 160^{\circ}$, and since $\triangle EDH$ is isosceles we have $H\hat{E}D = H\hat{D}E = 10^{\circ}$ and you can find all angles from here.