0

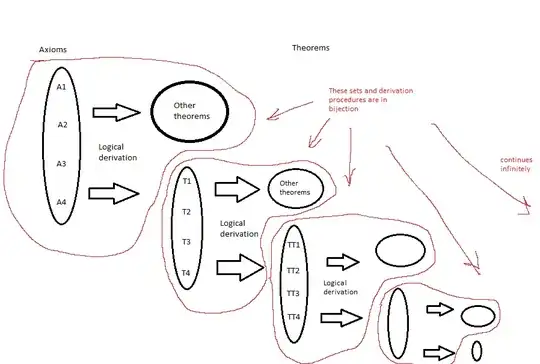
Does there exist a consistent theory (formal system) which has, say

  • a set of axioms $\{A_1,A_2,\dots, A_n\}$ + rules of inference

such that there is

  • a proper subset of (non-trivial) theorems $\{T_1,T_2, \dots,T_n\}$

which if taken themselves as axioms with the same rules would reproduce the whole theory itself?

In naive words: is there a consistent theory which contains "itself" as a part in a self-similar (like a fractal) manner?

Is ZFC such a theory?enter image description here

Sergey Dylda
  • 511
  • What is "self-similar" about this? Lots of theories admit multiple different axiomatizations. – Qiaochu Yuan Aug 22 '23 at 03:14
  • @QiaochuYuan Let me put it more simply, is there a theory which can be constructed inside itself in a non-trivial manner? Can we construct ZFC theory as a proper subset of ZFC theory itself? – Sergey Dylda Aug 22 '23 at 03:37
  • This is completely dependent on the choice of axiomatization of the theory. Some axiomatizations of ZFC - including the usual one - are redundant, and any theory has a redundant axiomatization (this is completely trivial - just add "$\varphi\wedge\varphi$" as an axiom where $\varphi$ is already an axiom); however, every theory has an irredundant axiomatization (see here). Does this answer your question? (I don't really see anything "fractal-like" about this.) – Noah Schweber Aug 22 '23 at 03:40
  • @NoahSchweber Your example about $\varphi \wedge \varphi$ is a nice one, but what I would call a "trivial case". I am sorry, I am not a logician I don't know how to described it in words more precisely. I've attached a picture to a post of what I have in mind. – Sergey Dylda Aug 22 '23 at 04:13
  • @bof ${T_1, \dots, T_n}$ is a proper subset of the set of all theorems derivable from axioms ${A_1, \dots A_n}$. Please look at the attached picture for example. – Sergey Dylda Aug 22 '23 at 04:29

1 Answers1

2

Every single propositional calculus which has CpCqp (this is in Polish notation) as an axiom has this property (or stronger system, so for example, any first-order predicate calculus also has this property).

A consequence solely of CpCqp is CpCqCrq. But, from CpCqCrq, CpCqp can get derived in a single detachment. Thus, anytime that CpCqp gets used as an axiom, CpCqCrq could replace it as an axiom and we have the same theorems (given that we have at least three variables). Unless you have a small number of variables, there are many, if not infinite also, theorems that could work similarly, since there's a sort of pattern of consequences from CpCqp which work out similarly...

CaCpCqp

CaCbCpCqp

.

.

.

Ca$_1$Ca$_2$...Ca$_n$CpCqp.

So, the answer to your question, ends up 'yes', at least without the 'non-trivial' part, of which I'm not sure what that means.

Doug Spoonwood
  • 11,211