4

According to the Wikipedia page of Benford’s Law:

Benford's law was empirically tested against the numbers (up to the 10th digit) generated by a number of important distributions, including the uniform distribution, the exponential distribution, the normal distribution, and others.

One of the most common distributions in Nature is the Poisson Distribution. However, this distribution is not mentioned in the Wikipedia article. Does the Poisson distribution satisfy Benford’s Law?

Riemann
  • 783

2 Answers2

4

No, it does not. The Wikipedia article states that "In short, Benford’s law requires that the numbers in the distribution being measured have a spread across at least an order of magnitude"; the source article states that "Roughly speaking, this means that small numbers have to be predominant. That is, when thinking of real-world data, conformity to the NBL necessitates a majority of small objects."

But the Poisson distribution doesn't behave this way. For large $\lambda$, $Poisson(\lambda)$ will have most of its mass within a few multiples of $\sqrt{\lambda}$ of the mean $\lambda$; in particular most draws from $Poisson(\lambda)$ will have the same first digit as $\lambda$ itself, or maybe one less or one more.

Furthermore the source article seems to only include continuous distributions and the Poisson is a discrete distribution. But I know of no reason that a discrete distribution couldn't follow Benford's law. One of the examples in Benford's original paper was street addresses, which are obviously discrete (although related to the continuous distribution of the lengths of the streets).

Michael Lugo
  • 22,354
  • How about small $\lambda$? – Riemann Aug 28 '23 at 20:11
  • 1
    @Riemann . Use python and simulate the Poisson variables (for any $\lambda$ you like) and see if they satisfy Benford's law. Here is described how to do it. It could hardly be simpler. – Kurt G. Aug 29 '23 at 07:43
  • Ok I checked: for $\lambda$ smaller than 5, more than 99% of the values is smaller than 10 and thus it does not satisfy Benford’s law – Riemann Aug 29 '23 at 09:59
  • @Riemann This does not sound very convincing. Benford makes a statement about leading digits, not about values. Leading digits are $1,...,9$ and therefore 100% of them are smaller than 10. :) – Kurt G. Aug 29 '23 at 16:42
2

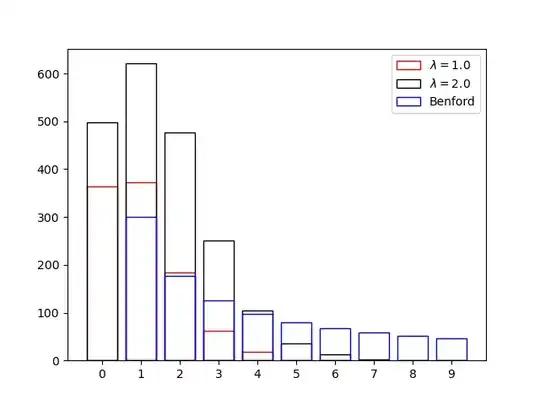
For small $\lambda$ a simulation in python shows that the leading digits of Poisson distributed integers $n$ do not satisfy Benford's law.

  • A lot of $n$ are zero thus having a zero as leading digit. Benford's law does not apply to that case.

  • For $\lambda=1$ the leading digit $2$ is reasonably well matched with Poisson, and for $\lambda=2$ the leading digit $4\,,$ but this is as good as it gets.

enter image description here

from numpy import random
import matplotlib.pyplot as plt

def get_leading_digit( s ):
    l = len(s)
    for i in range(0,l):
        if s[i] != '0' and s[i] != '.' and s[i] != '-':
           return( int(s[i]) )
    return( 0 )


x =    [ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ]
benf = [ 0, 301, 176, 125, 97, 79, 67, 58, 51, 46 ]
sim =  [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
ec = ['blue','red','black']
for lam in [1,2]:
    p = random.poisson(lam,1000)
    for i in range(len(p)):
        d = get_leading_digit(str(p[i]))
        sim[d] += 1
        if( d == 0 ):
            print( p[i], d )
        print( sim )
    plt.bar( x, sim, fill=False, label=r"$\lambda = ${:3.1f}".format(lam), edgecolor=ec[lam] )
plt.bar( x, benf, fill=False, label="Benford", edgecolor='blue' )
plt.xticks(x)
plt.legend()
plt.show()
Kurt G.
  • 14,198