2

I am not a mathematician, but I know that a sphere projected on the image plane becomes an ellipse under perspective transformation.

I don't know whether the ray starting from the center of projection passing through the center of the ellipse also passes through the center of the sphere.

According to this image, I would say no. But I am not sure. If not, how can I find the ray which passes through the center of a sphere given the 2D image coordinates of the ellipse? The camera is calibrated and I know the size of the sphere.

enter image description here

UPDATE

Here is a visual representation of David K's excellent answer:

enter image description here

NMO
  • 151
  • The rays from eye tangent to the sphere form a cone in space. However the same cone is formed by a family of spheres having varying diameter. Hence one cannot find the center of a unique sphere just knowing the intersection of the cone with the image plane. You need to say more about what you hope to determine about the sphere center from the image, for example maybe just find out the ray from the eye on which the sphere center lies. – coffeemath Aug 30 '23 at 10:37
  • You are right. Thanks for the comment. What I mean is the ray which passes through the center of the sphere. Does this ray also pass through the center of the ellipse? I changed the title and question accordingly. – NMO Aug 30 '23 at 13:06

1 Answers1

2

You can construct a line through the center of the sphere if you know the center of the projection and if you can identify the axes of the ellipse.

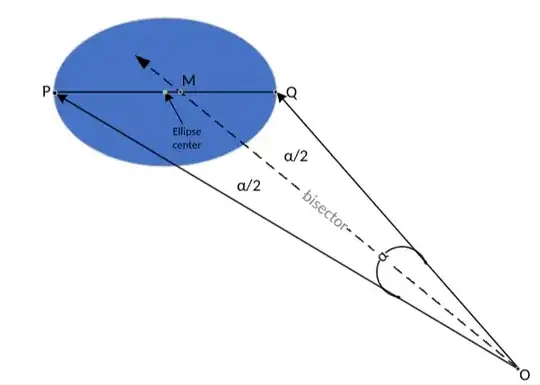
Let $O$ be the center of the projection and let $P$ and $Q$ be the endpoints of the major axis of the ellipse. Construct the lines $OP$ and $OQ$. These lines lie along the surface of the cone. The plane containing these lines also contains the axis of the cone. Bisect the angle $\angle POQ$. Then the angle bisector is the axis of the cone and passes through both the center of the projection and the center of the sphere.

The angle bisector of $\angle POQ$ intersects the major axis of the ellipse at a point $M$ that divides the major axis into two segments whose lengths have the ratio $\lvert MP\rvert:\lvert MQ\rvert = \lvert OP\rvert:\lvert OQ\rvert$. This implies that $M$ is the center of the ellipse only if $\lvert OP\rvert = \lvert OQ\rvert$, in which case the ellipse is a circle.

If you know the radius and location of the sphere then it is possible to find the point $M$ using that information.

If you know only the ellipse then it is not possible to identify the point $M$ where the axis of the cone intersects the plane of the ellipse. This is because there are infinitely many points that could be the center of a projection mapping a sphere to the given ellipse. See the answers to From ellipse equation to circular cone axis.

David K
  • 98,388