I need help with the following mathematical task:
A particle moves in the xy-plane according to the following rules:
- U: (m, n) → (m+1, n+1)
- L: (m, n) → (m+1, n-1)
where m and n are integers. I need to solve the following sub-problems:
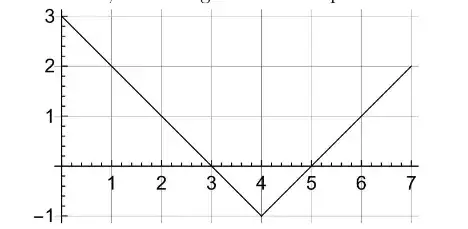
(a) How many paths are there from (0,3) to (7,2)? Please explain the method and provide all such paths. For example, the path corresponding to the given figure is LLLLUUU.
(b) How many paths from (0,3) to (7,2) touch or cross the x-axis at least once? Explain and print all such paths.
(c) How many paths from (0,3) to (7,2) never touch or cross the x-axis? Explain and print all such paths.
(d) How many paths are there from (5,5) to (30,10) that never touch or cross the x-axis? Please explain your solution.
(a): By counting the number of "U" and "L" steps required and using the binomial coefficient C(7,3) (7 choose 3), which gives 35, I found that there are 35 different paths for this subproblem.
(b) I am encountering difficulties with subproblem (b). I attempted to differentiate between cases where 3 "L" steps are required, followed by 1 "U" step, and cases where 4 "L" steps are needed, followed by 2 "U" steps. However, I struggled to calculate the total number of permutations. I assume that one should use the binomial coefficient to count the number of paths in each case. The consensus appears to be 7 paths, but I'm uncertain.
(c): I assume the answer here should be 35 - which was the answer in (b).
(d): Uncertain here.