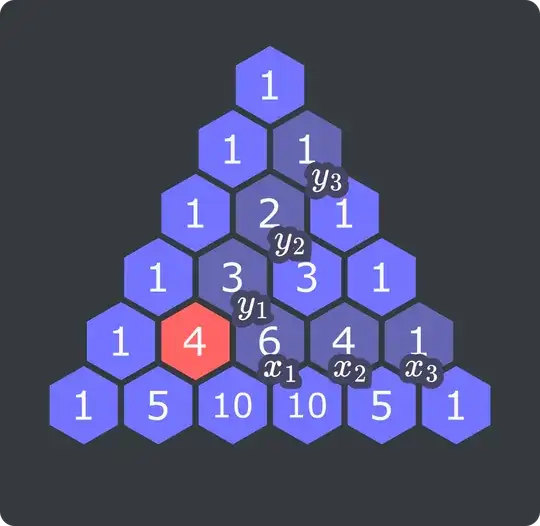
Dappy is playing around with Pascal's Triangle. While looking for patterns, he finds one equality that he likes a lot:
Pick any spot on Pascal's Triangle that isn't part of the right edge. Call the elements which are to the right of this spot on the same row $x_{k}$, such that $x_{1}$ denotes the position right next to the picked spot, and $x_{n}$ denotes the rightmost element on the row (which would be part of the right edge).
Similarly, denote by $y_{k}$ the elements going in the upwards-right direction.
Help Dappy prove that
$\sum_{k=1}^{n} (-1)^{k+1} x_{k} y_{n-k+1} = 1.$