Is there a name for functions that have multiple minima such that all minima are equal/one minima is less than another?

Question

Is there a name for a concept like that I can search? I am completely okay if there is no name so far.

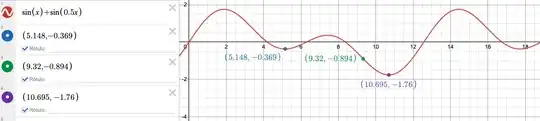
For example, $f\left(x\right)=\sin\left(x\right)$ has infinite minima, but they are all at $f\left(x\right)=-1$. On the contrary, $f\left(x\right)=\sin\left(x\right)+\sin\left(.5x\right)$ also has infinite minima, but some are at $f\left(x\right)\approx-.369$ while some are at $f\left(x\right)\approx-1.76$.

For now I have been calling them "stable" and "unstable" functions for now. Any suggestions?

EDIT: From the comments for one of the answers, I feel like "recurrent absolute minimum" and "recurrent non-absolute minimum" are the terms I will use for now.

The problem I am working on is something with optimization, figuring out if I can use any local minimum as my absolute minimum. The thing is, its also constrained to a set range for all inputs, so while there will be multiple local minima, I wouldn't say there are infinite.

Answer 1

I don't know if there is a name for that. But you could call them "periodic minimals" or "frequent minimals" since they apear periodically (or frequently). In the case of $f(x)=sin()+sin(.5)$, the "periodic minimal" has the form $f^{-1}(-1.76) + k4\pi$ for any $k \in \mathbb{Z}$.

On the other hand, it is not true when you say that $f(x) \approx -.369$ is also a periodic minimal, in the sense that $f(f^{-1}(-.369) + k4\pi) \leq f(x)$ for any $k \in \mathbb{Z}$ and for any $x \in \mathbb{R} \setminus \{x \in \mathbb{R} \, : \, x = f^{-1}(-1.76) + k4\pi\}$, ¿what about the green dot?

I guess you mean $f^{-1}(-.369) + k4\pi$ has zero derivative in those points, in that case you can define it as "frequent local minimum" or "periodic local minimum" and the definition is the same idea as the first paragraph.

Answer 2

tl; dr: The terms absolute minimum, and relative minimum or local minimum, are commonly-used for what you're calling "stable" and "unstable" minima, sometimes with the qualifier strict when suitable.

---

For a real-valued function $f$ whose domain is a set $X$ of real numbers (usually an interval or union of intervals), a point $x_{0}$ of $X$ is often called:

• An absolute minimum of $f$ if $f(x_{0}) \leq f(x)$ for all $x$ in $X$.
• A relative minimum or local minimum of $f$ if there exists a positive real number $r$ such that $f(x_{0}) \leq f(x)$ for all $x$ in $X$ with $|x - x_{0}| < r$.

Sometimes one wants to avoid or forbid the possibility of "non-uniqueness" of minima, and calls $x_{0}$:

• A strict absolute minimum of $f$ if $f(x_{0}) < f(x)$ for all $x$ in $X \setminus \{x_{0}\}$ (i.e., for all $x \neq x_{0}$).
• A strict local minimum of $f$ if there exists a positive real number $r$ such that $f(x_{0}) < f(x)$ for all $x$ in $X \setminus\{x_{0}\}$ with $|x - x_{0}| < r$.

The "absolute" terms make sense as-is for real-valued functions on an arbitrary set; the "local" terms extend almost without modification to real-valued functions on a topological space, where there is a notion of "neighborhoods."