24

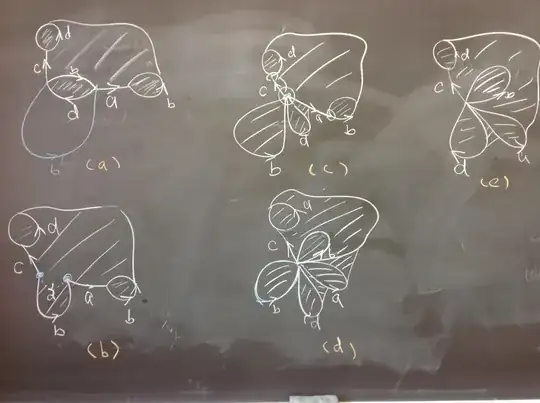
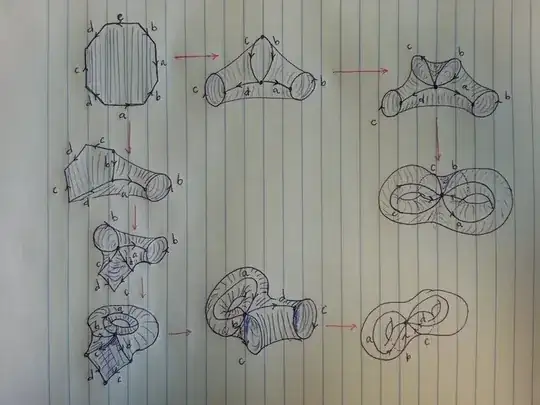
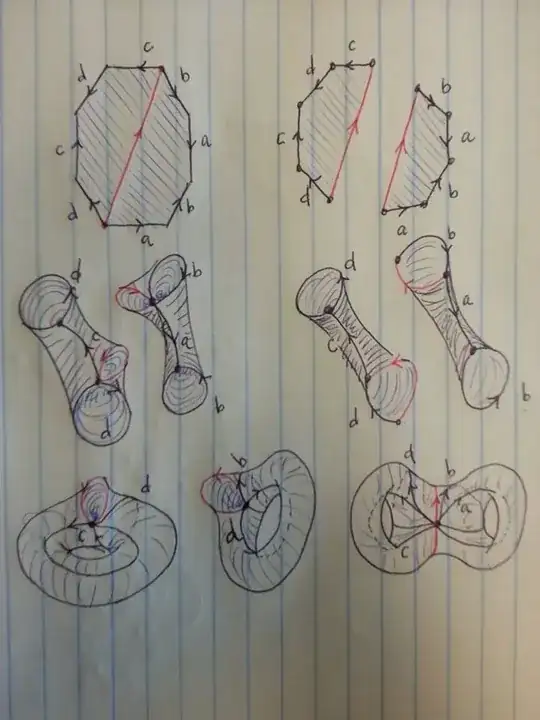
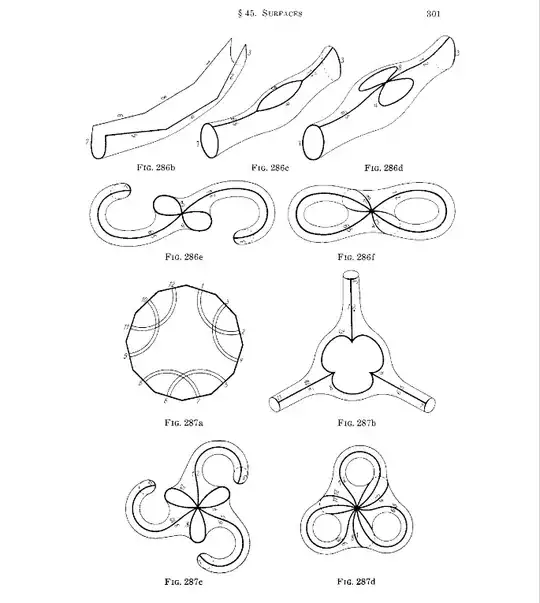
I am requesting some help or reference for visualization?

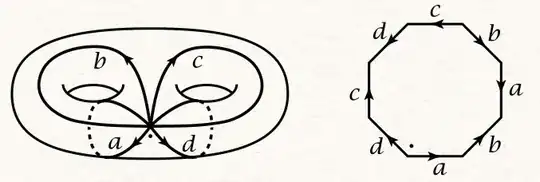
I am having a hard time constructing a genus 2 surface from 8-gon. May I request for some reference? Here's the construction I used from Hatcher: enter image description here

And here's my doodle.... I think I didn't get the identification of $b$ correctly at step (c), since I believe it $a$ shall go around the tube... enter image description here

2240
  • 131
  • 6
1LiterTears
  • 4,572
  • 4
    One way is to "cheat", cutting the octagon diagonally, into two pieces, one with $c$ and $d$, the other with $a$ and $b$. Then each piece is a torus (minus a disk), and you can then glue them back together. –  Aug 29 '13 at 20:02
  • Oh, that makes sense, @SteveD. Thank you. – 1LiterTears Aug 29 '13 at 20:08
  • I know this thread is really old, but I've recently found a reference that has a very nice picture explaining how to make a double torus from an octagon by identifying opposite sides. Have a look at pages 137-138 of http://dx.doi.org/10.1016/0370-1573(86)90159-6 – Iordan Iordanov Apr 03 '17 at 10:02

3 Answers3

48

Here are two visualizations. ${}{}{}{}{}{}{}{}{}{}$

two ways of making a genus-two surface from an octogon

Here's a third, from Steve D's comment: third way

Neal
  • 32,659
7

You can find this too on p. 301 of Hilbert & Cohn-Vossen "Geometry and the Imagination."

enter image description here

Agol
  • 929
  • 6
  • 13
2

On this page about classification of surfaces (unfortunately only in Frnech) you will find a collection of videos showing how to glue n-gons to get genus-g surfaces

http://analysis-situs.math.cnrs.fr/Classification-des-surfaces-triangulees-par-reduction-a-une-forme-normale.html

Guiheneuf
  • 31
  • Welcome to math SE. Could you edit your post to include the main idea in your link? Here, only a link is consider as a bad answer since if the link is broken, we lose that solution. – Alain Remillard Dec 10 '19 at 13:47