The $n$th urinal number is the $(n+1)$th Fibonacci number

Question

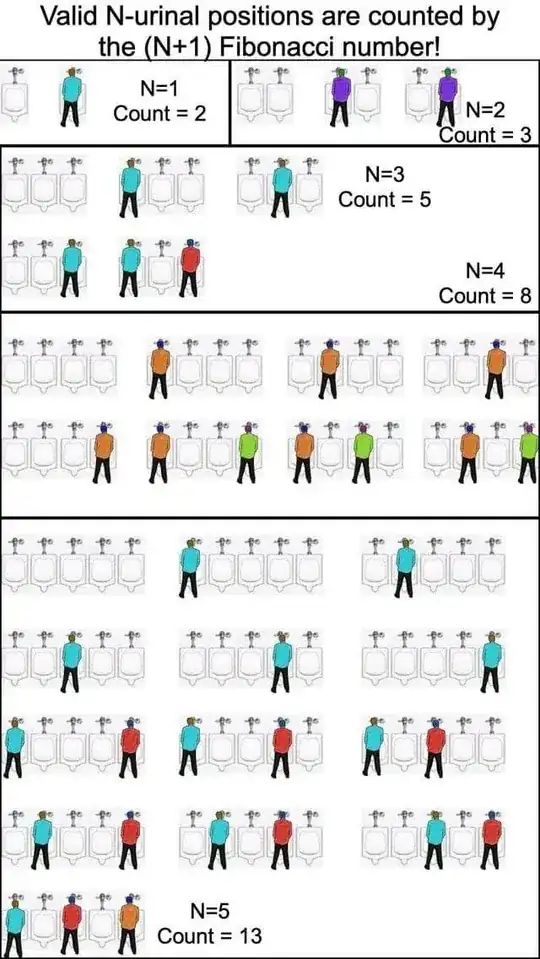
This post is inspired by a joke on a meme page which claims/conjectures that the number of "allowed" occupations of $n$ adjacent urinals is the $(n+1)$th Fibonacci number $F(n+1)$. Since it is generally not considered "gentlemanly" to occupy a urinal right next to one already in use, this number of allowed occupations is not equal to $2^n$. See below:

For example, if there's one urinal, then there are two possible occupations: the one urinal is either empty or in use. If there are two, there are three possible occupations: both empty, or either one in use. Both in use are not allowed by the above principle. Three urinals have five occupations: empty (1), one of the three in use (3) or only the outside urinals in use (1). You can check that four urinals have eight occupations. Etc.

Perhaps the problem deserves or already has a more academically appropriate name, but I could not find one. I will answer this question myself but if there are alternative solutions, let them come!

Answer 1

Let's think of this in terms of recurrence relations.

Let's call the $n$th urinal number $U(n)$.

We have base cases: $U(1)=2$, $U(2)=3$.

Now let's assume we know all urinal numbers till $U(n)$, and let's try to find $U(n+1)$.

Consider n+1 urinals marked as follows: _ _ _ ... n urinals ... _ _ _ (n+1)th urinal.

We have two mutually exculsive and exhaustive cases: Either the (n+1)th urinal is occupied, or it is not.

If the $(n+1)$th urinal is not occupied, we have fixed the occupancy status of $1$ urinal, and the remaining urinals have $U(n)$ possible configurations.

If it is occupied, then the $n$th urinal cannot be occupied - so we have fixed the occupancy of $2$ urinals, and $n-1$ adjacent urinals have $U(n-1)$ configurations.

Thus, we arrive at $U(n+1)=U(n)+U(n-1)$

Answer 2

It is a known result that $$F(n) = \sum_{k = 0}^{\lfloor n/2 \rfloor} {n - k \choose k }.$$ For example, $ F(2) = {2 \choose 0} + {1 \choose 1} = 2,$ $F(3) = {3 \choose 0} + {2 \choose 1} = 3$, $F(4) = {4 \choose 0} + {3 \choose 1} + {2 \choose 2} = 5$, etc. See How to show that this binomial sum satisfies the Fibonacci relation? .

Suppose we are looking at $n$ urinals. It is not so hard to show that there are can be at most $\lfloor (n+1)/2 \rfloor$ occupied urinals without there being any adjacent occupied:

• If $n$ is even, then $\lfloor (n+1)/2 \rfloor = n/2$. If there were $n/2 + 1$ people at the urinals and we divide the urinals in $n/2$ groups: urinal 1 and 2 in the first group, urinal 3 and 4 in the second group, etc., we find with the pigeonhole principle that there is at least one group that has two people in it, which cannot be since they are adjacent then.

• If $n$ is odd, this number is $(n+1)/2$. This case is somewhat similar to the above case and not too hard so I'll omit it.

So if we have $k$ occupied urinals, with $0 \leq k \leq \lfloor (n+1)/2 \rfloor$, it suffices to show that there are ${n+1 - k \choose k}$ ways to do this; it suffices to show that if we have $n$ adjacent boxes on a piece of paper, there are ${n+1 - k \choose k}$ ways to color $k$ boxes without coloring two adjacent boxes.

To do this, first suppose we have we have $n-k$ squares on the piece of paper, with $n-k + 1$ empty spaces: $n-k -1$ empty spaces between them and $2$ spaces at the outsides. Now, choosing a urinal configuration corresponds to choosing $k$ empty spaces and putting a cross on their position: the crosses correspond to occupied urinals and the squares to open urinals. E.g., the following is a choosing of $k = 2$ among $n = 7$ urinals: $$\square \times \square \square \times \square \square$$ Thus, the possible configurations with $k$ fixed is $n+1 - k \choose k$. This is true for each $0 \leq k \leq \lfloor (n+1)/2$, so $$U(n) = \sum_{k=0}^{\lfloor (n+1)/2 \rfloor} {n+1 - k \choose k} = F(n+1).$$