0

While solving a PDE using the Eigenfunction expansion method, I approximated the following function with an infinite sum: $$ f(x) = (1-x)e^{-kx} = \sum_{n=0}^\infty A_n \cos(w_nx) \tag 1 $$ where $x \in [0, 1]$, $w_n=(n+1/2)\pi$, and: $$ A_n = 2 \frac{e^{-k}}{\!\Big(k^2+w_n^2 \Big)^{\!2}} \Bigg(\!\! \Big(k^2-w_n^2 \Big) \cos(w_n) + e^k \Big(k^2(k-1) + w_n^2(k+1)\Big) - 2kw_n\sin(w_n)\!\Bigg) \tag 2$$

I made a graph to check my approximation. It seems correct as shown below. I call the function without the infinite sum a closed from function. The graph is constructed for $k=30$ and $n_{max} = 100001$. I used $100$ points for the $x$ axis.

Graph

I know that if $k$ tends to infinity that this function will be defined as:

$$ \lim_{k \to \infty} f(x)=\Bigg \{\begin{matrix} 1 & \text {if} & x=0\\ 0 & \text {if} & x>0 \end{matrix} \tag 3$$

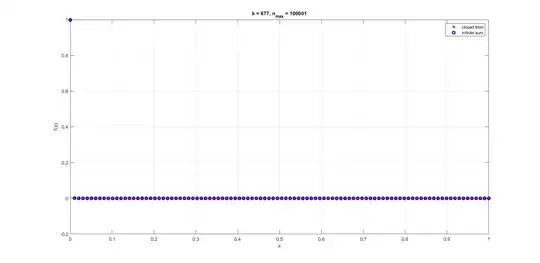
which I also checking using the graph given below, where $k$ was changed to $677$:

Plot

I wanted to prove that the infinite sum converges to $1$ if $x=0$ and $k$ tends to infinity:

$$ \lim_{k \to \infty} f(0) = \lim_{k \to \infty} \sum_{n=0}^\infty A_n = \sum_{n=0}^\infty \lim_{k \to \infty} A_n =1 \tag4$$

I was hoping that after I reformulate the expression for $A_n$ as $k$ tends to infinity, it would be easy to prove that the infinite sum converges to $1$.

I rewrote the expression for $A_n$ as:

$$A_n = B_n+C_n+D_n \tag 5$$

where:

$$ B_n = 2{ e^{-k}\Big(k^2-w_n^2 \Big) \cos(w_n) \over \Big(k^2+w_n^2 \Big)^2} \tag 6$$

$$C_n = 2{ k^2(k-1)+w_n^2(k+1) \over \Big(k^2+w_n^2 \Big)^2} \tag 7$$

$$D_n = -4{ e^{-k} kw_n\sin(w_n) \over \Big(k^2+w_n^2 \Big)^2} \tag 8$$

Next, I tried solving $$\lim_{k \to \infty} A_n = \lim_{k \to \infty}B_n + \lim_{k \to \infty}C_n + \lim_{k \to \infty}D_n \tag 9$$

The first term is easy to solve because $\cos(w_n)$ is equal to zero since $w_n$ represents the roots of the cosine function:

$$ \lim_{k \to \infty}B_n = \lim_{k \to \infty}2{ e^{-k}\Big(k^2-w_n^2 \Big) \cdot 0 \over \Big(k^2+w_n^2 \Big)^2}=0 \tag {10}$$

I solved the second term by multiplication of the enumerator and demoninator with $1/k^4$:

$$ \lim_{k \to \infty}C_n = \lim_{k \to \infty}2{k^3-k^2+kw_n^2+w_n^2\over k^4+2k^2w_n^2+w_n^4}=\lim_{k \to \infty}2{{1 \over k} - {1 \over k^2} + {w_n^2 \over k^3} + {w_n^2 \over k^4}\over 1 + {2w_n^2 \over k^2}+{w_n^4 \over k^4}}=0 \tag {11}$$

Also, I calculated: $$ \lim_{k \to \infty}D_n = \pm 4{ e^{-k} kw_n \over \Big(k^2+w_n^2 \Big)^2} = 0 \tag{12} $$

I thought I made a mistake somewhere in my calculations of $B_n$, $C_n$ and $D_n$ as $k$ tends to infinity. However, I tried plotting $B_n$, $C_n$ and $D_n$ with respect to $k$ for $n = \{0, 1, 2 \}$. It really does seem that they tend to zero as $k$ gets bigger as shown in the graphs below:

matrix

However, that seems to me like a contradiction to the fact that $f(0) = 1$. So my question is, where did I go wrong here? How can I prove that the inifinite sum defined by $(4)$ is equal to $1$ and did I really calculate the limits correctly or not?

Sammy Black
  • 25,273
FriendlyNeighborhoodEngineer
  • 1,014
  • 1
    why do you think you can switch series like this, so in other words why do you assume that $\lim_{k \to \infty} \sum_{n=0}^\infty A_n = \sum_{n=0}^\infty \lim_{k \to \infty} A_n =1 $? you can easily prove that $\sum_n A_n(k)=1$ for each $k$ but the limit of $A_n(k)$ is $0$ and that is not a contradiction since the sum is not absolutely convergent as $|A_n(k)| \approx 1/n$ – Conrad Nov 17 '23 at 19:56
  • 1
    note that your $f$ extended periodically in an appropriate way to have a Fourier expansion of the type you consider will have some type $1$ discontinuities and the coefficients are relatively big then (cannot be $o(1/n)$) so phenomena like this happen generally – Conrad Nov 17 '23 at 20:05
  • You're right, I made a mistake assuming that the sum and the limit can change places. I just checked the links given in the comments of this question: https://math.stackexchange.com/questions/23057/under-what-condition-we-can-interchange-order-of-a-limit-and-a-summation

    First, I should prove that the sum converges to $1$ regardless of the value of $k$, which would actually even cover the case where $k$ tends to infinity.

    Thank you @Conard. Would you please write an answer so I can accept it?

     – FriendlyNeighborhoodEngineer Nov 17 '23 at 20:12
  • 1
    are u sure that the computation above is right? – Conrad Nov 17 '23 at 22:55
  • I think it is. I used Matlab for checking. The results were consistent. – FriendlyNeighborhoodEngineer Nov 18 '23 at 10:10
  • 1
    Yes I realized that I was incorrect since I thought the $w \sin w$ inside the smaller bracket and then I was getting that the conjugate (Fourier sense) series was divergent at $1$ and that is plainly not the case when you compute the extension on $[-2,2]$ for which the above is the Fourier series; so I corrected the answer, as actually $\sum A_n(k)$ is absolutely convergent but not dominated by an absolutely convergent one for all $k$ as $\sup_k |A_n| \sim 1/n$ – Conrad Nov 18 '23 at 15:18
  • Noted. Thank you for all your efforts :D – FriendlyNeighborhoodEngineer Nov 19 '23 at 13:22
  • 1
    It's an interesting problem and a bit subtler than I thought – Conrad Nov 19 '23 at 15:18

1 Answers1

1

Note that $M(n)=\sup_k |A_n(k)| \approx 1/n$ as in the OP notation $|C_n|$ behaves like that while the rest are $O(1/n^2)$ so the series $\sum_n M(n)$ diverges which means that switching limits and series is not justified and indeed is incorrect as $\sum_n A_n(k)=1$ for every $k$ but $\lim_k A_n(k)=0$ for every $n$.

($\sum_n A_n(k)=1$ easily follows since for fixed $k$ the series is actually absolutely convergent)

Conrad
  • 27,433