How do you find the value of $\sum_{n=1}^{\infty} (-1)^{n+1}\frac{1}{n^2}$?

Question

Extra information which may be useful is that $\sum_{n=1}^{\infty} \frac{1}{n^2}$ equals $\frac{\pi^2}{6}$ (Euler's solution to the Basel Problem).

Answer 1

(Evaluating the sum without using the extra information) We will express the sum

\begin{align*} \sum_{n=1}^\infty (-1)^{n+1} \frac{1}{n^2} \end{align*}

via a complex contour integral. It employs the fact that the function

\begin{align*} \dfrac{1}{\sin \pi z} \end{align*}

has simple poles at all integers $n$, as we now verify:

\begin{align*} \dfrac{1}{\sin \pi z} & = \dfrac{1}{\sin \pi [n + (z-n)]} \nonumber \\ & = \dfrac{1}{(-1)^n [\pi (z-n) - \frac{1}{3!} \pi^3 (z-n)^3 + \cdots]} \nonumber \\ & = (-1)^n \dfrac{1}{(z-n) \pi [1 - \frac{1}{3!} \pi^2 (z-n)^2 + \cdots]} \nonumber \\ & = (-1)^n \dfrac{1}{(z-n) \pi} [1 + \frac{1}{3!} \pi^2 (z-n)^2 + \cdots] \nonumber \\ & = (-1)^n \dfrac{1}{(z-n) \pi} + \cdots \end{align*}

This allows us to write

\begin{align*} \sum_{n=1}^\infty (-1)^{n+1} \frac{1}{n^2} = -\frac{1}{2 i} \oint_C \dfrac{1}{z^2 \sin \pi z} dz \end{align*}

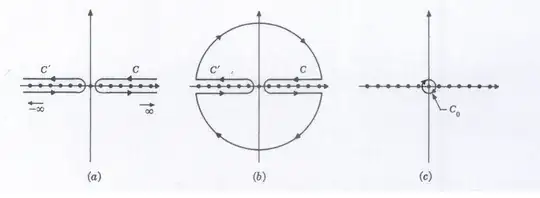
where the contour $C$ is defined in fig (a).

We have

\begin{align*} \sum_{n=1}^\infty (-1)^{n+1} \frac{1}{n^2} & = \frac{1}{2} \sum_{n=1}^\infty (-1)^{n+1} \frac{1}{n^2} + \frac{1}{2} \sum_{n=-1}^{-\infty} (-1)^{n+1}\frac{1}{n^2} = - \frac{1}{4 i} \oint_{C+C'} \dfrac{1}{z^2 \sin \pi z} dz \end{align*}

where the contour $C'$ is defined in fig (a). We complete the path of integration along semicircles at infinity (see fig (b)) since the integration along them vanishes. Since the resulting enclosed area contains no singularities except at $z=0$, we can shrink this contour down to an infinitesimal circle $C_0$ around the origin (see fig (c)). So that

\begin{align} \sum_{n=1}^\infty (-1)^{n+1} \frac{1}{n^2} = - \frac{1}{4 i} \oint_{C_0} \dfrac{1}{z^2 \sin \pi z} dz \end{align}

Expanding the integrand around $z=0$ and isolate the $z^{-1}$ term to obtain the residue. Then

\begin{align} \dfrac{1}{z^2 \sin \pi z} = \dfrac{1}{z^2 (\pi z - \frac{1}{3!} \pi^3 z^3 + \cdots)} \end{align} \begin{align} = \dfrac{1}{z^3 \pi (1 - \frac{1}{6} \pi^2 z^2 + \cdots)} \end{align} \begin{align} = \dfrac{1}{z^3 \pi} (1 + \frac{1}{6} \pi^2 z^2 + \cdots) \end{align} \begin{align} = \cdots + \dfrac{\pi}{6} \frac{1}{z} + \cdots \end{align}

So that

\begin{align*} \sum_{n=1}^\infty (-1)^{n+1} \frac{1}{n^2} = -\frac{1}{4 i} \oint_{ C_0} \dfrac{1}{z^2 \sin \pi z} dz = -\frac{1}{4 i} (-2 \pi i) (\dfrac{\pi}{6}) = \frac{\pi^2}{12} \end{align*}

Answer 2

More generally, let $s(m) =\sum_{n=1}^{\infty} \dfrac{(-1)^{n+1}}{n^m} $. (Yours is $m=2$.)

Then

$\begin{array}\\ s(m) &=\sum_{n=1}^{\infty} \dfrac{(-1)^{n+1}}{n^m}\\ &=\sum_{n=1}^{\infty} \dfrac{1}{(2n-1)^m}-\sum_{n=1}^{\infty} \dfrac{1}{(2n)^m}\\ &=\sum_{n=1}^{\infty} \dfrac{1}{(2n-1)^m}+\sum_{n=1}^{\infty} \dfrac{1}{(2n)^m}-2\sum_{n=1}^{\infty} \dfrac{1}{(2n)^m}\\ &=\sum_{n=1}^{\infty} \dfrac{1}{n^m}-\dfrac1{2^{m-1}}\sum_{n=1}^{\infty} \dfrac{1}{n^m}\\ &=(1-\dfrac1{2^{m-1}})\sum_{n=1}^{\infty} \dfrac{1}{n^m}\\ &=(1-\dfrac1{2^{m-1}})\zeta(m)\\ \end{array} $

Yours is the case $m=2$ so the result is $(1-\dfrac1{2})\zeta(2) =\dfrac{\pi^2}{12} $.

Answer 3

$A = \sum\frac{1}{n^2} = [odd+even] = \sum \frac{1}{(2n+1)^2} + \frac{1}{(2n)^2}$. $S = \sum(-1)^{n+1}\frac{1}{n^2} = [odd-even]=\sum \frac{1}{(2n+1)^2} - \frac{1}{(2n)^2} = A-2\sum \frac{1}{(2n)^2} = A - \frac{1}{2}\sum\frac{1}{n^2} = A/2 = \frac{\pi^2}{6\cdot 2}.$

A simpler way of stating this is $S = odd-even=odd+even-2even = A - \frac{1}{2}\sum\frac{1}{n^2} = A/2.$