2

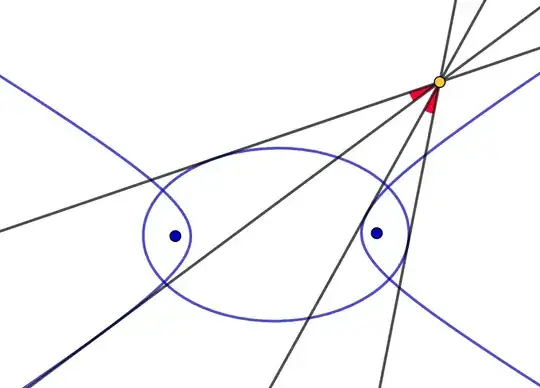
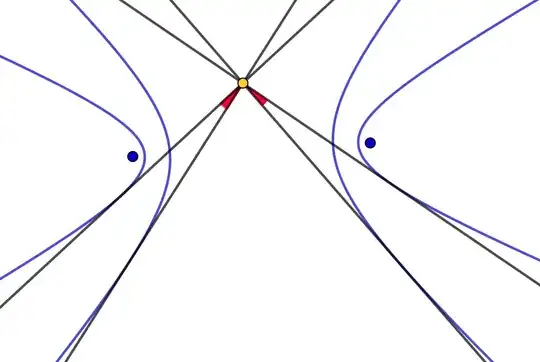
While playing on GeoGebra a while ago, I came across a feature of conic sections that seems somewhat elementary. I don't know if it was previously discovered or not.

If we have two conic sections with common foci and we draw their tangents passing through a point in the same plane, then the measures of the angles between these tangents will be equal.

Here are some illustrations: enter image description here enter image description here enter image description here enter image description here

And if you can prove that that would be nice

زكريا حسناوي
  • 2,296
  • 2
    Nice observation! ... It follows from the property that, for a single conic $c$ and point $P$, the lines through $P$ tangent to $c$ and the lines through $P$ and the foci of $c$ make congruent angles. See, for instance, this (decade-old!) question (which only mentions the case of ellipses). – Blue Dec 09 '23 at 14:55
  • 1
    Thank you. Indeed, the property becomes immediate after observing this. All it takes then is to prove the first property for all conic sections. – زكريا حسناوي Dec 09 '23 at 14:59
  • There's probably a slick synthetic approach to the general result, but it can also be proven with a bit of calculus and some tedious vector work using, eg, the parameterization $$P(\theta)=\frac{p}{1+e\cos\theta}(\cos\theta,\sin\theta)$$ where $e$ is the (arbitrary) eccentricity and $p$ is the semi-latus-rectum. This conic has one focus at the origin and the other at $\left(\dfrac{2ep}{e^2-1},0\right)$. The tangents at, say, $P(2\theta)$ and $P(2\phi)$ meet at $$\frac{p}{\cos(\theta-\phi)+e\cos(\theta+\phi)}(\cos(\theta+\phi),\sin(\theta+\phi))$$ The rest is left as an exercise to the reader. – Blue Dec 09 '23 at 16:21
  • 1
    See my comment to this question. – Jean Marie Dec 09 '23 at 22:51
  • Thank you so much – زكريا حسناوي Dec 09 '23 at 23:41

0 Answers0