So I was thinking of a particular problem the other day and started experimenting with it. It goes like this:
I want to find natural numbers $x$ and $y$ such that:
$x$ is an $n$-digit number, and $y$ is an $m$-digit number, where $n$ and $m$ are not necessarily equal. Let their digit representations be $x = a_1a_2...a_n$ and $y = b_1b_2...b_m$, where all $a_i$ and $b_j$ are between $0$ and $9$, except for $a_1$ and $b_1$. Neither $a_1$ nor $b_1$ can be equal to $0$.
Also, let $x'$ have the digit representation $a_{1}a_{2}...a_{n} 2$, and $y'$ have $b_1b_2...b_m2$. I call $x'$ and $y'$ the "lazy squares" (hehe) of $x$ and $y$ if the following holds true: $$x^2 + y^2 = x' + y'.$$
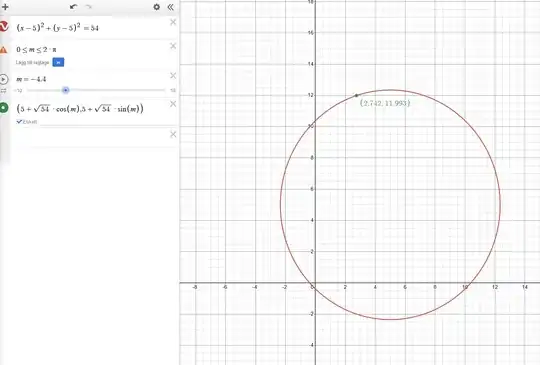
In general this seems tedious and hard. What I have done thus far is trying a simpler case, supposing that both $x$ and $y$ are $1$-digit numbers. Now their only digits are simply $x$ and $y$ respectively. This yields the following equation: $$x^2+y^2 = 10x+10y+4 .$$ After some algebraic manipulations we can rewrite the equation as the equation of a circle in the following way: $$(x-5)^2+(y-5)^2 = 54.$$
Now, I came to the conclusion that this equation does not have any natural numbered solutions just by eye-balling it in desmos. I guess you could do an exhaustive solution/proof by making a program in python for instance and just check for all $1$-digit $x$'s and $y$'s and come to the same conclusion.
So... I am wondering if there might be a simpler solution or approach to the general problem that I'm not able to see? If not, I'm wondering how one could take a stab att the more general case where $x$ and $y$ are $n$-digit and $m$-digit natural numbers respectively?