this question follows one from yesterday that got deleted because it was a duplicate.
The problem was about solving this equation (in $ℚ[x]$) :
$$f(x)(2x^3 + 3x^2 + 7x + 1) + g(x)(5x^4 + x + 1) = x + 3$$
Members of the community answered yesterday that the gcd is 1 which implies that the equation is solvable.
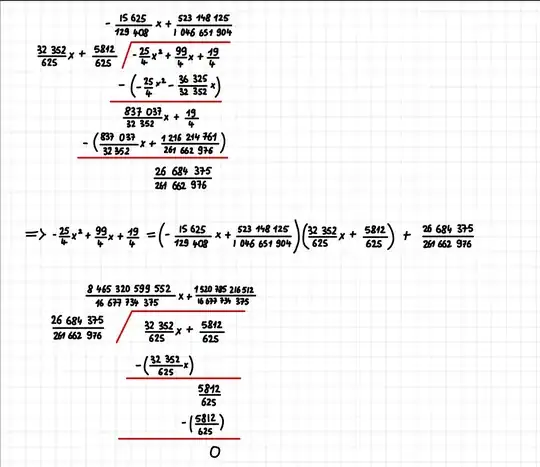
Based on their advices I tried to use Extended Euclidian Algo for polynomials to find the Bezout coeff such that $a(x)(2x^3+3x^2+7x+1)+b(x)(5x^4+x+1) = 1$.
But after very long calculations, I couldn't find 1 as the last reminder but $\frac{26684375}{261662976} \simeq 0.102$. I hope it's a miscalculation, but I'm lost.
Can you tell me how members that answered me yesterday found 1 as the gcd that quickly ?