The proof of Vinogradov that $U_{p^{\alpha}}$ ($\alpha \geq 1$) is cyclic for an odd prime $p$, has a part that I don't understand.
We take $g$ a primitive root of $U_p$.
And, at a certain point of the proof, Vinogradov says:
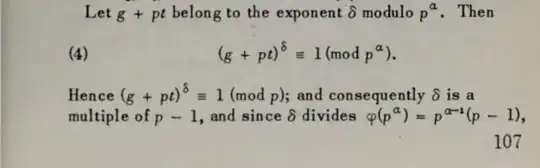
I don't understand how he gets that $\delta = p^{r-1} (p-1)$.
I understand that $\delta \mid p^{r-1} (p-1)$ for any $1\leq r\leq \alpha$.
But my problem is to prove the other divisibility, namely: $$p^{r-1} (p-1) \mid \delta \tag{1}$$.
My guess on this is that there are two possible ways of proving $(1)$.
First way would be to prove that $p^{r-1} \mid \delta$ for every $1\leq r\leq \alpha$. Then, as $p^{r-1}$ is prime with $(p-1)$ (and as $p-1 \mid \delta$) we could arrive to the desired result $(1)$.
Second way would be to use an order argument i.e. to prove that $p^{r-1} (p-1)$ is the order of some element and that this same element raised to the power $\delta$ is congruent to $1$. I still haven't figured out if this second way would take place modulo $p$ or modulo $p^{\alpha}$. Nonetheless, I doubt this could happen modulo $p$ because in $U_p$, $p-1$ is already the maximal order that we can have, so how could $p^{r-1} (p-1)$ be a valid order ?
PS: Here is the beginning of the proof:
In this beginning of the proof, the equalities in the left bracket might help to use an "order argument" (the second way) but I don't really know how.
Thanks
