The following image is from Geometric Series Proofs: An Annotated Bibliography.
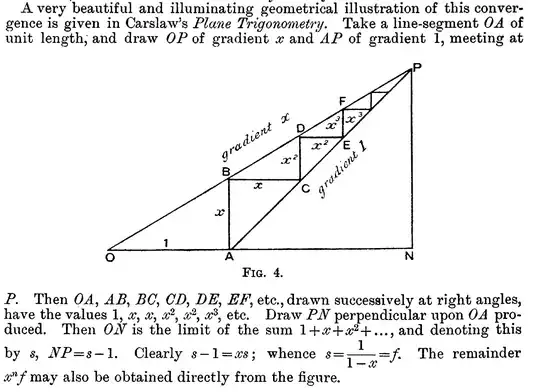
Please explain why it is said that:
"$ON$ is the limit of the sum $1+x+\dots$."
Thank you.
Edit: I guess what through me off was the word "limit"!
The following image is from Geometric Series Proofs: An Annotated Bibliography.

Please explain why it is said that:
"$ON$ is the limit of the sum $1+x+\dots$."
Thank you.
Edit: I guess what through me off was the word "limit"!
Notice that the horizontal lines of length $1,x,x^2,x^3,\ldots$ union to form a line of length $ON$.
There are two ways to travel the horizontal distance from $O$ to $N$. The easiest way is to go via the line $ON$. Alternatively, you could follow the staircase, only counting the movement in the horizontal direction. The first stair has horizontal movement $1$, the second has horizontal movement $x$, and so on. However, once you've arrived at $N$, it shouldn't matter which way you went, the distances are the same. Therefore (the length of the line segment) $ON$ is the same as the limit of the sum $1 + x + x^2 + \dots$
Not really an answer to the question. If anyone objects I'll delete it.
I came across this trying to find an alternative expression for $\Delta$ in the picture. I thought it looked kinda nice. Similar to the picture above but not exactly the same.
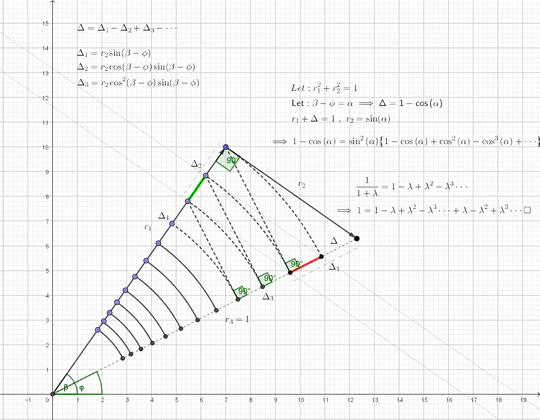
The length marked as $\Delta$ in the picture is of course simply: $1-\cos{(\beta-\phi)}$. Looking for an alternative way to calculate $\Delta$ we get the geometric series:
First approximate $\Delta$ as $\Delta_1$. Now we have to subtract the red part in the picture. Going over to the other side we see $\Delta_2$ contains the length of that red part but has an additional part (the green part in the picture). If we subtract that and repeat this process infinitely we must get $\Delta$.
This results in :
$1-\cos{(\beta-\phi)}=\sin^2{(\beta-\phi)}\left\{ 1-\cos{(\beta-\phi)} +\cos^2{(\beta-\phi)} -\cos^3{(\beta-\phi)} + \cdots \right\} \implies $
$ \frac{1-\cos{(\beta-\phi)}}{\sin^2{(\beta-\phi)}} = \frac{1-\cos{(\beta-\phi)}}{1-\cos^2{(\beta-\phi)}}= \frac{1-\cos{(\beta-\phi)}}{(1+\cos{(\beta-\phi)})(1-\cos{(\beta-\phi)})} = $
$ \frac{1}{1+\cos{(\beta-\phi)} }= 1-\cos{(\beta-\phi)} +\cos^2{(\beta-\phi)} -\cos^3{(\beta-\phi)} + \cdots $
The geometric series.