Find the distance between 2 lines

Question

Question

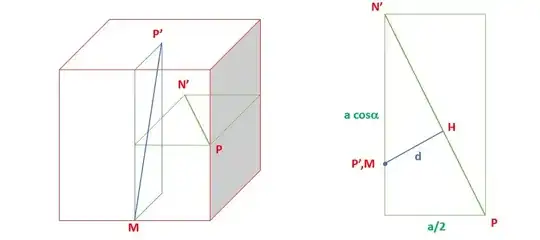
Let the cube $ABCDA' B' C' D'$ be where the points $M$ and $P$ are the midpoints of the edges $(AB)$ and $(B B')$ and $P'$ and $N'$ the centers of the faces $A' B' C' D'$ respectively $CDD' C'$ . Calculate the distance between the lines $M P'$ , and $P N'$ , according to the edge of the cube $AB = a$ , where $a$ is strictly positive real number.

My idea

I know that this type of problems are solved expressing the volume in $2$ ways.

So using one of the volume formula we get that $$ V(MP'N'P)=\frac{N'P\cdot MP'\cdot \operatorname{dis}(MP',N'P)\sin\angle (MP', N'P)}{6} $$

We can easily express that $MP'=N'P=\frac{a \sqrt{5}}{2}$ and $ \angle (MP', N'P)= \frac{\sqrt{21}}{50}$ and to find the distance wanted i have to express the volume of the tetrahedron again.

I thought of showing what procent of its volume is from the volume of the cube which is equal to $a^3$, but i dont know how.

Hope one of you can help me! Thank you!

Answer 1

Here is a detailed computation of the volume of our tetrahedron.

The face $MN'P'$ of the tetrahedron $MN'P'P$ lies on a plane parallel to the cube face $AA'DD'$ and passing through the center of the cube. The area of triangle $MN'P'$ is equal to $$ \frac{3a^2}{8}. $$ The altitude from the vertex $P$ to the face $MN'P'$ is $a/2$. Therefore, the volume of the tetrahedron is $$ \frac{1}{3}\cdot \frac{3a^2}{8}\cdot\frac{a}{2}=\frac{a^3}{16}. $$

Adding.

In the figure, the plane passing through the center of the cube and parallel to $ADD'A'$ is green. The points $M$, $P'$, $N'$ lie on this plane. The altitude $PQ$ of the tetrahedron from vertex $P$ to face $MP'N'$ must be perpendicular to the green plane and $PQ=a/2$.

Answer 2

We can fix a coordinate system with origin at $M$ such that

• $M=(0,0,0)$
• $N'=(0,a,a/2)$
• $P(a/2,0,a/2)$
• $P'(0,a/2,a)$

then

• line $MP'$ has parametric equation: $t(0,a/2,a)$
• line $PN'$ has parametric equation: $(a/2,0,a/2)+s(-a/2,a,0)$

with $t,s \in \mathbb R$, then we can find its distance as explained for example here:

• Find shortest distance between lines in 3D

Answer 3

Here is another way without using coordinates.

As first step let consider a rotation of the cube around the edge containing $M$ by an angle $\alpha=\arctan \frac 1 2$ such that line $MP'$ is vertical.

Looking from the top, the distance $d$, by triangle similarity, is such that

$$\frac{d}{\frac 34 a \cos \alpha}=\frac{\frac a 2}{\sqrt{\frac{a^2}4+a^2\cos^2 \alpha}}\implies d=\dfrac{ 3 a }{2 \sqrt{21}}$$

using that $\cos\left(\arctan \frac12\right)=\frac 1{\sqrt{1+\left(\frac 1 2\right)^2}}=\frac 2 5 \sqrt 5$.

Answer 4

If you take

$ A = (0,0,0) , B = (1, 0, 0), C = (1,1,0), D = (0, 1, 0) $

Then

$ A' = (0,0,1) , B' = (1,0,1), C' = (1,1,1), D' = (0,1,1) $

It follows that

$ M = (0.5, 0, 0) , P = (1, 0, 0.5), P' = (0.5, 0.5, 1), N' = (0.5, 1, 0.5) $

Line $MP'$ is

$ L_1(t) =M + t (MP') = (0.5,0,0) + t (0, 0.5, 1) $

and line $PN'$ is

$ L_2(s) = P + s (PN') = (1, 0, 0.5) + s (-0.5 , 1 , 0 ) $

The cross product of the direction vectors is

$ F = (0,0.5,1) \times (-0.5, 1, 0) = ( -1 , -0.5, 0.25 ) $

The plane containing $M$ and having a normal $F$ is

$ F \cdot (p - M ) = 0 $

Hence the required distance is

$ d = \dfrac{ | F \cdot (N' - M) | }{ \sqrt{ F \cdot F } } $

This is equal to

$ d = \dfrac{ | (( -1 , -0.5, 0.25 ) \cdot (0, 1, 0.5 ) | }{ \left(\sqrt{\dfrac{21}{16}} \right)} $

And this simplifies to

$ d = \dfrac{3}{2 \sqrt{21} } $

This is for a cube for side length $1$. If the side length is $a$ , then

$ d = \dfrac{ 3 a }{2 \sqrt{21}} $