Proving $\int_0^\infty\frac1{1+e^{px}}dx=\frac{\ln2}p$

Question

My table of integrals states that $$\int_0^\infty\frac1{1+e^{px}}dx=\frac{\ln2}p$$ Where the real part of $p$ is greater than $0$. At first, I thought that I could integrate along the rectangular contour, but the pole is on its boundary. Then thought of drawing the semicircular contour with some angle $\theta$ in between its two radii, but that will enclose an infinite amount of poles. So how can I go about solving this integral using complex analysis?

I found that $u=1+e^{px}$ is the simplest way when I saw a question similar to this one (read what's next before putting a close vote). Unfortunately, it's closed and none of the answers use complex analysis.

Answer 1

For $p>0$ we have:

$$\int_{0}^{\infty}\frac{1}{1+e^{px}}dx=\frac{1}{p}\int_{0}^{\infty}\frac{p\,e^{px}}{e^{px}(1+e^{px})}dx$$

Change $u=e^{px}$ and take the integral

$$\frac{1}{p}\int_{1}^{\infty}\frac{1}{u(1+u)}du=\frac{1}{p}\int_{1}^{\infty}\left[\frac{1}{u}-\frac{1}{1+u}\right]du=\left[\frac{\ln u-\ln(1+u)}{p}\right]_{1}^{\infty}=\frac{\ln 2}{p}$$

since $$\lim_{u\to \infty}(\ln u-\ln(1+u))=\lim_{u\to \infty}\ln\left(\frac{u}{1+u}\right)=0.$$

Answer 2

Visit vertices $0,\,X,\,X+\frac{2\pi i}{p},\,\frac{2\pi i}{p}$ in that order as $X\to\infty$:$$\oint\frac{\left(z-\frac{\pi i}{p}\right)\mathrm{d}z}{1+e^{pz}}\to-\frac{2\pi i}{p}\int_0^\infty\frac{\mathrm{d}x}{1+e^{px}}-\int_0^{\frac{2\pi i}{p}}\frac{z-\frac{\pi i}{p}}{1+e^{pz}}\mathrm{d}z.$$As we enclosed no poles,$$\int_0^\infty\frac{\mathrm{d}x}{1+e^{px}}=\int_0^{\frac{2\pi i}{p}}\frac{\frac12+\frac{ip}{2\pi}z}{1+e^{pz}}\mathrm{d}z\stackrel{z=\frac{2i}{p}(\pi-u)}{=}\frac{1}{p\pi}\int_{-\pi/2}^{\pi/2}u\cot u\mathrm{d}u.$$We're done.

Note that as $p$ may not be real this contour is a parallelogram, but not necessarily a rectangle.

Answer 3

For any $p>0$,the integrand can be expressed as an infinite series. $$ \begin{aligned}\int_0^{\infty} \frac{1}{1+e^{p x}} d x = & \int_0^{\infty} \frac{e^{-p x}}{1+e^{-p x}} d x \\ = & \sum_{n=0}^{\infty}(-1)^n \int_0^{\infty} e^{-(n+1)px} d x \\ = & \sum_{n=0}^{\infty}(-1)^n\left[\frac{e^{-(n+1) p x}}{-(n+1) p}\right]_0^{\infty} \\ = & \sum_{n=0}^{\infty} \frac{(-1)^n}{(n+1) p} \\ = & \frac{\ln 2}{p } \end{aligned} $$

Answer 4

Okay, so I've given this (what i would consider) a comprehensive try, and got some results. However, I warn you that they are very cumbersome and redundant, as the complex analysis here still relies on real evaluation methods that can just be used to solve the integral directly, and sometimes more. (Sometimes is an understatement here actually lmao)

The integral we want to find with complex analysis is $$I = \int_0^\infty\frac1{1+e^{ax}}\text{ d}x$$

When we see an integrand such as $\frac1{1+e^{ax}}$ with the objective of contour integrating, we should immediately think "rectangular contour", as the poles are along the imaginary axis. However, we cannot directly take the integrand as our complex function, as on a rectangular contour, the top and bottom contours will cancel out without a proper numerator (try it if you dont believe me lol)

Instead, let's try the function $\displaystyle f(z)=\frac{e^{bz}}{1+e^{az}}$ where $b=0$ in $$J(b)=\int_0^\infty \frac{e^{bx}}{1+e^{ax}}\text{ d}x$$ will give us our desired integral $J(0)=I$.

Consider the contour below, where the pole shown is at some $\pi i\over a$. The rectangular contour goes from the origin to $z=R$, then up to $z=R+\frac{2\pi i}{a}$, then left to $z=\frac{2\pi i}{a}$, down to $z=\frac{\pi i}{a}+\varepsilon$, around in a small arc of radius $\varepsilon$ to avoid the pole, and then back down to the origin.

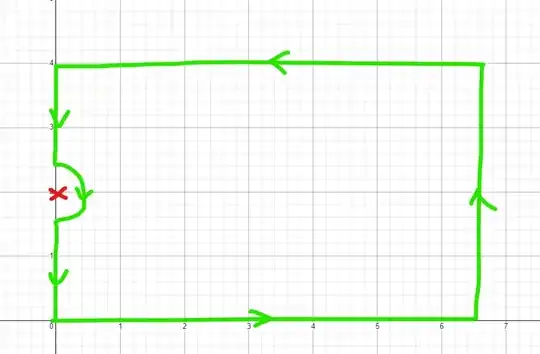
(I'm assuming you have some experience with contour integrals, so I'll skip the parameterization, DCT limit passing arguments, etc)

The bottom path reduces to $J(b)$, the right path goes to $0$, the top path gives us a $-e^{\frac{2\pi ib}{a}}$ multiple of $J(b)$, and the small arc gives $\frac{\pi i}{a}e^{\frac{\pi i b}{a}}$ after using DCT to pass the limit. However, the straight left-side paths gives us the principal value integral $$PV\int_\frac{2\pi}{a}^0 \frac{ie^{biy}\text{ d}y}{1+e^{aiy}}$$ after taking the $\varepsilon$ limit.

Solving this integral utilizes techniques such as hypergeometric function/series, and we cannot avoid this by taking real or imaginary parts either since the numerator isn't nice. This defeats the purpose of contour integration.

We can try another function with a nice numerator $\displaystyle f(z) = \frac{e^{itz}}{1+e^{az}}$ such that $t=0$ in $$K(t) = \int_0^\infty \frac{e^{itx}}{1+e^{ax}} \text{ d}x$$ gives us our integral. The numerator is "nice" because the added $i$ under the imaginary/real parts function could simplify into trig, and make the resultant integrand "nice" (this is a standard trick ofc). We use the same contour as above.

This results in the bottom path being $K(t)$, right going to $0$, top being $K(t)$ scaled by $-e^{\frac{-2\pi t}{a}}$, and the small arc being $\frac{i\pi}a e^{\frac{-\pi t}a}$ after DCT and limit passing. The left straight paths still give a principal value integral $$PV\int_{2\pi \over a}^0\frac{ie^{-ty}\text{ d}y}{1+e^{aiy}}$$ This integral is once again unsolvable without hypergeometric functions/series, but we can try passing imaginary and real part functions.

As it turns out, if we pass the imaginary part over it, the integrand of the principal value integral actually cancels out into a very nice $e^{-ty}\over 2$. HOWEVER, the imaginary part also reduces $K(t)$ down to $$\Im K(t) = \int_0^\infty {\sin(tx)\over 1+e^{ax}} \text{ d}x$$ for which $t=0$ does not work, since it gives the numerator a value of $0$ instead of the desired $1$. This is not what we want.

We can pass the real part function instead, and get a cosine on $K(t)$, which does reduce the numerator of the integrand down to 1 when $t=0$, $$\Re K(t) = \int_0^\infty {\cos(tx)\over 1+e^{ax}} \text{ d}x \iff \Re K(0) = I$$ However, this also reduces the principal value integral's integrand to $\frac12 e^{-ty}\tan(ay/2)$, which decidedly does not integrate well, so this defeats the purpose of contour integration. You can hard bash the result, but really, is this what you're aiming for?

Probably not.
(also idk where that negative came from, probably some small algebra error i couldnt catch earlier but w/e im not running the principal value again it took so long lol)

Lastly, just for the sake of it, you could directly use the function $\displaystyle f(z) = \frac1{1+e^{az}}$ with the contour

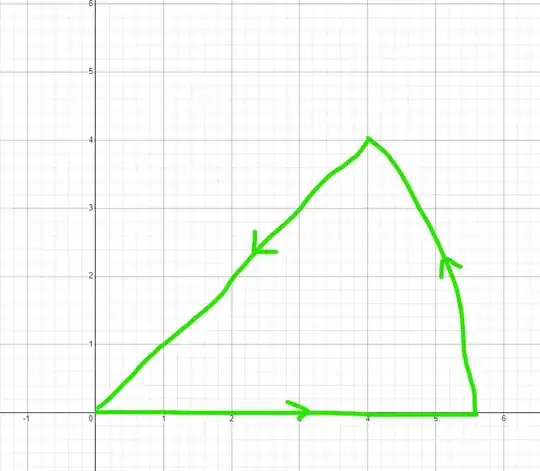
to directly get a result in terms of $I$ by avoiding the two cancelling rectangular paths. This contour here is a pizza slice of 45 degrees, going from the origin to $z=R$, then in a 45 degree arc counterclockwise, and then back to the origin. This contour avoids dealing with any of the pole or principal value shenanigans at all, by staying away from the imaginary axis.

Here, the outer arc goes $0$, and the bottom path gives our integral.
(verifying the outer arc does indeed go to 0 can be done manually when we pass the limit inside using DCT of couse, but I used mathematica, which gave a funny seemingly nonsense restriction shown below)

The remaining diagonal path then gives us the integral $$\int_\infty^0 \frac{e^{\pi i\over4}\text{ d}r}{1+e^{are^{i\pi\over4}}}$$ but to evaluate this, we legit have to use the same substitution/tricks we would have done if we evaluated our original integral $I$ directly, so this defeats the purpose.

So yea, as you can see, you can use contour integration. But, none of them are efficient/worth the effort, and none of them are "nice" really, since the rectangular contour integrals requires hypergeometric functions to evaluate (and polygamma i guess), or require the same substitution/tricks that you could've done on the original integral.

Does this satisfy your curiosity? ¯\_(ツ)_/¯

Also I realize I have been vague sometimes, since typing out all the work in latex will be absolutely horrendous lmao so treat it as an exercise if you are willing to give this a try yourself. If you need any elaboration though just tell me and I'll provide.

$\tiny{\text{im in pain help}}$