1

Let $A_1 A_2 \ldots A_n$ be a regular polygon with $n$ sides inscribed in a circle with center $O$. Calculate the sum of vectors $OA_1 + OA_2 + \ldots + OA_n$ when $n$ is odd.

I’ve tried this for a Triangle and a Pentagon and I think the sum is supposed to be $0$, but I’m not sure how to prove it for any odd $n$.

Proof for the Triangle

Victor Ban
  • 81
  • 5
  • 1
    Use complex numbers representation $A_k \leftrightarrow R e^{2i k \pi/n}$ and recognize the sum of a finite geometric series. – Jean Marie Feb 06 '24 at 15:21
  • 2
    rotate the polygon for $\frac{360^\circ}{n}$ wrt $O$, the sum of vectors will be rotated by same angle. However, this operation is equivalent to a relabeling of vertices, this means the sum is invariant under such a rotation and must be $0$. – achille hui Feb 06 '24 at 15:21
  • 1
    You can also use the fact that $\vec{OA_1} + \vec{A_1A_2} = \vec{OA_2}$. – sudeep5221 Feb 06 '24 at 15:23
  • Hello, I am in 9th grade and haven’t learned complex numbers yet. Also, I don’t get the solution by rotating the polygon. As for writing the vectors as that sum, in the end I got 0=0. – Victor Ban Feb 06 '24 at 15:28
  • Can you show your proof for the triangle and the pentagon? Unless you did something very fancy, you should be able to extend it from there. – Calvin Lin Feb 06 '24 at 15:34
  • Another hint (which might be what sudeep is implying): Show that the sum is equivalent to walking along the perimeter of another regular $n-$gon, where we land back at the origin, hence is equal to 0. – Calvin Lin Feb 06 '24 at 15:38
  • I have edited my post with the proof for the triangle. I didn’t write the one for the pentagon, but it’s basically the same, just more complicated. – Victor Ban Feb 06 '24 at 15:48
  • Please have a look at this. – MathRookie2204 Feb 06 '24 at 15:49
  • 2
    Write your sum under the form $\sum_{k=1}^n \frac12(\vec{OA_k}+\vec{OA_{k+1}})$ (with a cyclic numbering). Recognize in it a regular n-gon rotated and shrinked wrt the first one, with "shrinkage ratio" a certain fixed number $a<1$, then iterate the process : you end up with $0$... – Jean Marie Feb 06 '24 at 15:49
  • Have you already learnt about $\sin$, $\cos$, and some identities about them? – user103496 Feb 16 '24 at 06:08

1 Answers1

0

(I assume you're familiar with the unit-circle definitions of $\sin$ and $\cos$ and also some trigonometric identities.)

Let $O=\left(0,0\right)$, $A_{1}=\left(1,0\right)$, $A_{2}=\left(\cos\frac{2\pi}{n},\sin\frac{2\pi}{n}\right)$, $A_{3}=\left(\cos2\frac{2\pi}{n},\sin2\frac{2\pi}{n}\right)$, $\dots$, and $A_{n}=\left(\cos\left(n-1\right)\frac{2\pi}{n},\sin\left(n-1\right)\frac{2\pi}{n}\right)$.

Observe $A_{1}$, $A_{2}$, $\dots$, and $A_{n}$ are the vertices of the regular $n$-sided polygon centered on $O$.

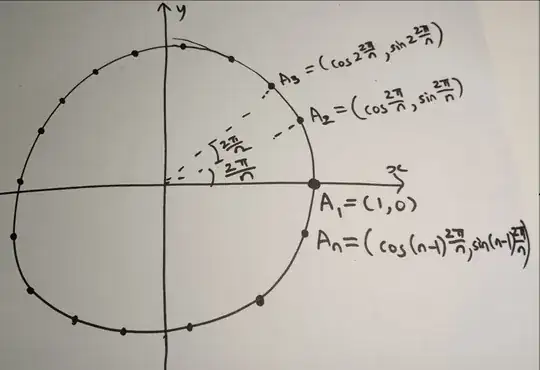
enter image description here

Let $\mathbf{S}=\overrightarrow{OA_{1}}+\overrightarrow{OA_{2}}+\dots+\overrightarrow{OA_{n}}=\left(S_{x},S_{y}\right)$.

Then $S_{x}=1+\cos\frac{2\pi}{n}+\cos2\frac{2\pi}{n}+\dots+\cos\left(n-1\right)\frac{2\pi}{n}$.

And, $S_{y}=0+\sin\frac{2\pi}{n}+\sin2\frac{2\pi}{n}+\dots+\sin\left(n-1\right)\frac{2\pi}{n}$.

It can be shown that $S_{x}=0$ (see here—I recommend Sasha's answer which uses only the Product-to-Sum Identity for Sine and Cosine).

It can be shown that $S_{y}=0$ (see here—I recommend user65203's answer).

Altogether, $\mathbf{S}=\left(0,0\right)$.

user103496
  • 108