$\mathcal M = \{z \in \mathbb C | |z|=r \}$ , where $r \in \mathbb R , r >0$

Question

The statement of the problem : Consider the set $\mathcal M = \{ z \in \mathbb C | |z|=r\} $ , where $r \in \mathbb R , r >0$

a) Prove that there exists $a,b \in \mathcal M,a \neq b$ such that $a+b \in \mathcal M$.

b) Find the values ​​of the positive integer $n \geq 2$ for which there exists a subset $\mathcal S \subseteq \mathcal M$, with n elements, so that $u+v \in \mathcal M , \forall u,v \in \mathcal S,u \neq v$.

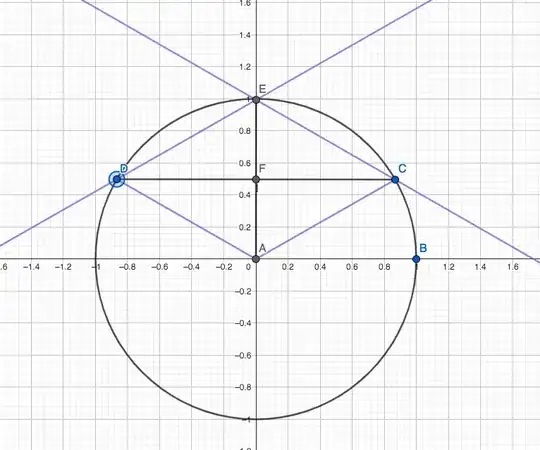
My approach: First of all, the set $\mathcal M$ consists of all the affixes of the points located on the circle with the center in the coordinate system and the radius r. To prove the point a), I chose a point on the axis $Oy$ with coordinates $(0,\frac{r}{2})$, then I took the parallel to the $Ox$ axis. It is obvious that this will intersect the circle in two points, symmetrical to the $Oy$ axis. According to the parallelogram rule, the sum of these affixes will be in $(0,r)$, which is on the circle, so I proved point a), below I put a picture that suggests my reasoning :

Now at b) I encountered some problems and I didn't really know which approach to take, but I think that the solution is also a geometric one.

Any and all proofs will be helpful. Thanks a lot!

Answer 1

The key idea is to use the position vectors of the points on the circle.

2 vectors with magnitude $r$ will add up to a vector with magnitude $r$ iff the angle between the vectors is 120°. So the angle between the position vectors of any pair of points in $\mathcal{S}$ should be 120°.

Also, as the sum of the angles about any point (the origin of the argand plane, in our case) is 360°, we can have at most three points in $\mathcal{S}$.

As a particular example, for $n = 3$, $\mathcal{S} = \{r, r\omega, r{\omega}^2\}$ works, where $\omega$ is the complex root of unity.

Answer 2

I take $r=1$, which doesn't change the generality of the problem.

Let $p,q \in \mathbb R$ such that $e^{i p}=u\neq v=e^{iq}$

$$u+v\color{red}{\textbf=}2\cos(\frac{p-q}2)e^{i\frac{p+q}2}\in \mathcal {M}\iff p-q=\pm\frac{2\pi}3$$ $\color{red}{\text{based}}$ on trigonometry formulas.

Then $v=ju$ or $v=j^2u$, with $ j:=e^{\frac{2i\pi}{3} }$

Let us then have a third point $w$ that meets our requirements: We have $w=j^2u $ or $w=ju$.

Our reasoning shows that the sets we are looking for belong to$$\{\color{red}{\{}\{u,ju\},\{u,j^2u\},\{u,ju,j^2u\}\color{red}{\}}, \text{with } u\in\mathcal M\}$$

$\text{The set of possible numbers is }\{2,3\}$.