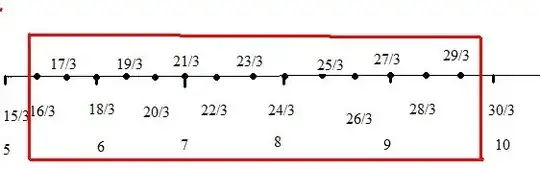
Between a number $5$ and $10$ on a number line,exclusive , a dark gray tick mark is placed at every multiple of $\frac{1}{3}$ and a light gray tick mark is placed at every multiple of $\frac{1}{9}$. At how many places will a dark gray tick mark and light gray tick mark overlap?
I can't see the systematic way of solving this. Can anyone provide a systematic way of approaching such a problem? The book I have its solution is not handy.
Every multiple of $\frac{1}{3}$ is also a multiple of $\frac{1}{9}$. Thus, there will be overlap at every multiple of $\frac{1}{3}$, of which there are $((10 - 5) * 3) - 1$ (Three greater than each of $5,6,7,8,9$, less the one mark at $10$.)
This gives a total of $14$.
You gonna have to solve this equation, because the number of ways the two ticks will overlap is $\frac{n}{3} = \frac{y}{9}$, but we can write $y=3n$
$$5 \leq \frac{n}{3} \leq 10$$ $$15 \leq n \leq 30$$
This means that there are 16 possible answers for n and the two ticks will overlap 16 times.
Multiply the numbers by $9$, then you have the range $45,\cdots,90$ exclusive, with the '$\frac{1}{9}$th' marks at every integer, and '$\frac{1}{3}$rd' marks at every multiple of $3$. Hence this reduces to finding all the multiples of $3$ in the (inclusive) range $48,\cdots,87$, which is quickly computed to be $\frac{87-48}{3}+1= 14$.
Concept : Overlap at LCM($\displaystyle\frac{1}{3}$,$\displaystyle\frac{1}{9}$) = $\displaystyle\frac{1}{3}$
Just take one interval 5 to 6
$5$ + $\displaystyle\frac{1}{3}$ , $5$ + $\displaystyle\frac{2}{3}$ , $5$ + $\displaystyle\frac{3}{3}=6$
so from $5$ to $6$ there are $3$ points ,
similary 3 points between $6$ to $7$ , $7$ to $8$ ,$8$ to $9$ , $9$ to $10$ (but 10 not included )
so $(5 \times 3 ) - 1$ =
$14$
