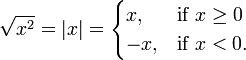How is it, that $\sqrt{x^2}$ is not $ x$, but $|x|$?

Question

As far as I see, $\sqrt{x^2}$ is not $x$, but $|x|$, meaning the "absolute". I totally get this, because $x^2$ is positive, if $x$ is negative, so $\sqrt{y}$, whether $y = 10^2$ or $y = -10^2$: $y$ is positive.

But then I remember that $\sqrt{x}$ is the same as $x^{1/2}$ and thus, $\sqrt{x^2}$ is the same as $x^{1}$.

So, as far as I get it, $\sqrt{x^2} = x^{2/2}$.

But then, I can cancel $\frac{2}{2}$ to $1$. So: $\sqrt{x^2} = x^1 = x$.

Where does the absolute value in this derivation of the calculation come from?

I get it why its there: Because $(-x)^2 = x^2$, so the radicand is always positive. But from $\sqrt{x^n} = x^{n/2}$ I dont understand how it gets there.

Answer 1

This is why you need to pay attention to the hypotheses of a theorem! The exponent laws you've learned are almost surely only for integer exponents or for positive bases: until you have learned multi-valued functions and complex exponentiation, you should always be suspicious whenever you're both using non-integers in exponents and negative numbers in bases in the same problem. (presumably, you'd understand the nuances once you've fully learned how to deal with complex analysis)

Answer 2

It is true that $\sqrt{x} = x^{\frac{1}{2}}$ and $(\sqrt{x})^2 = (x^{\frac{1}{2}})^2 = x$. This is true for all $x$ in the domain of $\sqrt{x}$, namely $x \in [0, \infty)$.

The absolute value comes from composing the square root and square in the opposite order; that is $\sqrt{x^2} = (x^2)^{\frac{1}{2}}$. For any $x \in \mathbb{R}$, $x^2 \geq 0$ so $x^2$ is in the domain of the square root function. The square root function however returns only non-negative values, so if $x < 0$, $(x^2)^{\frac{1}{2}} \neq x$ (but if $x \geq 0$, $(x^2)^{\frac{1}{2}} = x$). In fact, as you have noted, if $x < 0$ write $x = -a$ for some $a \in (0, \infty)$, then $x^2 = (-a)^2 = a^2$, so $(x^2)^{\frac{1}{2}} = (a^2)^{\frac{1}{2}}$. Now $a > 0$ so we obtain $(a^2)^{\frac{1}{2}} = a$, but $a$ is just the absolute value of $x$, i.e. $a = |x|$.

Answer 3

The principal square root function $f(x) = √x$ is a function that maps the set of non-negative real numbers onto itself. In geometrical terms, the square root function maps the area of a square to its side length. For all real numbers $x$,

Answer 4

The convention is that $\sqrt y$ is the non-negative square root. Now if you say $y=x^2$ you need to recognize that the result will be non-negative. To get that right, you need to say $\sqrt {x^2}=|x|$ When you see it printed, you just need to know the convention and go along with it. It is a source of errors when you are working problems, because when you write $\sqrt {x^2}$ you might not be thinking of this problem.

Answer 5

$√x$ = $(x)^{1/2}$ represents only the principle value of square root of x. Its the exponential representation of principle square root.

Principle square root: The non-negative (positive) square root of a number is called its Principal Square Root.

Thus, $√(x^2)$ = $(x^2)^{1/2}$ = x is the principle square root (positive)

While, $√(x^2)$ = $±x$ ; both positive and negaive square roots.