I have some problems in Discretize the second order derivative of this equation
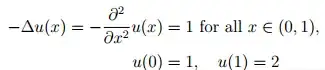
after I find u(x) by integrating it, I have problem in discretize it ,, I'm not mathematical person and I try to read a lot .
any help ?!
I have some problems in Discretize the second order derivative of this equation
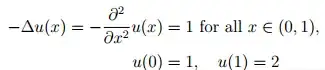
after I find u(x) by integrating it, I have problem in discretize it ,, I'm not mathematical person and I try to read a lot .
any help ?!
A discrete form of the second derivative is $$u''(x) \approx \frac{u(x+h)-2u(x)+u(x-h)}{h^2}\tag{1}$$ Partition the interval $[0,1]$ with uniformly distributed points $0=x_0<x_1<\dots <x_n=1$ and denote $u_j=u(x_j)$. Since $h=1/n$, the difference scheme for your equation takes the form $$ u_{j+1}-2u_j+u_{j-1} = -\frac{1}{n^2},\quad j=1,\dots,n-1 \tag{2}$$ Since $u_0=1$ and $u_n=2$ are known, the equations (2) form a linear system of $n-1$ equations with $n-1$ unknowns. Its solution is an approximation to $u$.
Maybe some users need help for the derivation of eq. (1) in the answer above.
One can proceed as follows: In the continuum case \begin{equation} p(x):=\frac{du}{dx}:=\lim_{h\rightarrow 0} \frac{u(x+h)-u(x)}{h} \end{equation} So for the second derivative \begin{equation} \frac{d^2u}{dx^2}=\frac{dp}{dx}=\lim_{j\rightarrow 0} \frac{p(x+j)-p(x)}{j} =\lim_{j\rightarrow 0} \frac{\lim_{h\rightarrow 0} \frac{u(x+h+j)-u(x+j)}{h}-\lim_{h\rightarrow 0} \frac{u(x+h)-u(x)}{h}}{j}=\lim_{h\rightarrow 0} \frac{ u(x+2h)-2u(x+h)+u(x)}{h^2} \end{equation} In the discrete version, $h$ becomes a small but finite parameter. Shifting once by $h$ yields the result. \begin{equation} \frac{d^2u}{dx^2}\approx \frac{ u(x+h)-2u(x)+u(x-h)}{h^2} \end{equation}
Closed formulas for higher discrete derivatives are given in the Wikipedia-article on finite differences.