3

Find this integral $$I=\int_{0}^{\frac{\pi}{2}}\cos{x}\sqrt{1+\tan{x}}dx$$

My try:I find this wolf can't find it. **

then I try: let $$\sqrt{1+\tan{x}}=t\Longrightarrow x=\arctan{(t^2-1)}$$ so $$I=\int_{1}^{+\infty}\cos{\left(\arctan{(t^2-1)}\right)}\dfrac{2t^2}{(t^2-1)^2}dt$$

Then I can't

Harry Peter
  • 7,819
  • Mathematica returns a value for the definite integral expressed in terms of the Meijer G function. – Lucian Nov 16 '13 at 16:32
  • @Lucian. If you want fun, just compute the antiderivative and post it ! – Claude Leibovici Nov 16 '13 at 16:41
  • I'm running FullSimplify[...] on that dreadful formula as we speak... :-) P.S.: I've posted, or at least mentioned, two such monsters on this post. – Lucian Nov 16 '13 at 16:46
  • It would be a good exercise for students to show that the improper integral is convergent. I am writing this one down! – imranfat Nov 16 '13 at 16:50
  • It maybe this integral can use Special constant,such as gamma,and Eluer constant,Catalan’s Constant and so on –  Nov 16 '13 at 16:52
  • 1
    Don't know if this will be helpful or not, but another equivalent form of the integral is $I = \int_0^{\infty}\frac{\sqrt{1+u}}{(1+u^2)^{\frac32}}\space du$. – David H Nov 16 '13 at 17:01
  • 1
    Another form of this integral is

    $$I=\int_{0}^{1}\sqrt{1+\frac{y}{\sqrt{1-y^{2}}}}\mathrm{d}y$$

    and maybe it can help.

     – Leonida Nov 16 '13 at 17:44

3 Answers3

6

$\newcommand{\+}{^{\dagger}}% \newcommand{\angles}[1]{\left\langle #1 \right\rangle}% \newcommand{\braces}[1]{\left\lbrace #1 \right\rbrace}% \newcommand{\bracks}[1]{\left\lbrack #1 \right\rbrack}% \newcommand{\dd}{{\rm d}}% \newcommand{\isdiv}{\,\left.\right\vert\,}% \newcommand{\ds}[1]{\displaystyle{#1}}% \newcommand{\equalby}[1]{{#1 \atop {= \atop \vphantom{\huge A}}}}% \newcommand{\expo}[1]{\,{\rm e}^{#1}\,}% \newcommand{\floor}[1]{\,\left\lfloor #1 \right\rfloor\,}% \newcommand{\ic}{{\rm i}}% \newcommand{\imp}{\Longrightarrow}% \newcommand{\ket}[1]{\left\vert #1\right\rangle}% \newcommand{\pars}[1]{\left( #1 \right)}% \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\pp}{{\cal P}}% \newcommand{\root}[2][]{\,\sqrt[#1]{\,#2\,}\,}% \newcommand{\sech}{\,{\rm sech}}% \newcommand{\sgn}{\,{\rm sgn}}% \newcommand{\totald}[3][]{\frac{{\rm d}^{#1} #2}{{\rm d} #3^{#1}}} \newcommand{\ul}[1]{\underline{#1}}% \newcommand{\verts}[1]{\left\vert #1 \right\vert}% \newcommand{\yy}{\Longleftrightarrow}$ $\ds{\large% I \equiv \int_{0}^{\pi/2}\cos\pars{x}\root{1 + \tan\pars{x}}\,\dd x:\ {\large ?}}$

\begin{align} I&=\int_{0}^{\pi/2}\root{\cos^{2}\pars{x} + \sin\pars{x}\cos\pars{x}}\,\dd x = \int_{0}^{\pi/2}\root{{1 + \cos\pars{2x} \over 2} + {\sin\pars{2x} \over 2}}\,\dd x \\[3mm]&= {1 \over 4}\,\root{2}\int_{0}^{\pi}\root{1 + \cos\pars{x} + \sin\pars{x}}\,\dd x = {1 \over 4}\,\root{2} \int_{0}^{\pi}\root{1 + \root{2}\sin\pars{x + {\pi \over 4}}}\,\dd x \\[3mm]&= {1 \over 4}\,\root{2} \int_{\pi/4}^{5\pi/4}\root{1 + \root{2}\sin\pars{x}}\,\dd x \end{align}

The $\it\underline{last\ integral}$ is evaluated here in terms of a Second Kind Elliptic function.

Felix Marin
  • 89,464
1

This is an awful integral ! The formula for the antiderivative write in several pages. The numerical value is : 1.3571445175439115954095406.

Claude Leibovici
  • 260,315
0

As I wrote earlier, its value is non-elementary, and expressible in terms of the Meijer G function:

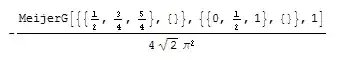
Image

The expression of its anti-derivative can be found here. It involves incomplete elliptic integrals of the first and second kind.

Lucian
  • 48,334
  • 2
  • 83
  • 154