The structure of countable ordinals

Question

Consider the recursively defined hyperoperation sequence $\circ_i$

$$\begin{array}{rcrclclcl} x& \small{+}&(y\ {\small+}1)&:=&x& &&{\small+}&1\\ x& \boldsymbol{+}&(y\ {\small+}1)&:=&(x& \boldsymbol{+} &y)&{\small+}&x\\ x& \cdot &(y\ {\small+}1)&:=&(x& \cdot& y)&\boldsymbol{+}&x\\ x&\uparrow &(y\ {\small+}1)&:=&(x&\uparrow& y)&\cdot&x\\ x& \uparrow\uparrow &(y\ {\small+}1)&:=&(x&\uparrow\uparrow& y)&\uparrow&x\\ &&&\vdots\\ x& \uparrow^{n+1} &(y\ {\small+}1)&:=&(x&\uparrow^{n+1}& y)&\uparrow^{n}&x\\ &&&\vdots\\ \end{array}$$

with $x \circ_0 y = x {\small+} 1$ (the successor function), $x \circ_1 y = x + y$, $x \circ_2 y = x \cdot y$, $x \circ_3 y = x \uparrow y = x^y$, and so on. This sequence can be used to define a sequence of successor functions for ordinals:

$$\begin{array}{rcrclclcl} \mathsf{S}_0(x) &:=& x \circ_0 \omega&=&x&\small{+}& \omega& = &x& \small{+}& 1\\ \mathsf{S}_1(x) &:=& x \circ_1 \omega&=&x&\boldsymbol{+}& \omega\\ \mathsf{S}_2(x) &:=& x \circ_2 \omega&=&x&\cdot& \omega\\ \mathsf{S}_3(x) &:=& x \circ_3 \omega&=&x&\uparrow& \omega\\ &\vdots\\ \end{array}$$

With these successor functions and their respective limits one gets the following picture of the countable ordinals (at least the smaller ones):

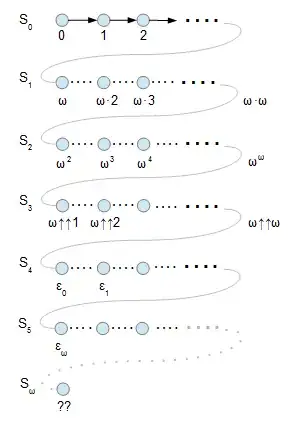
Note that the small dots on every level correspond to the big dots on the level before.

Is this picture essentially correct and maybe helpful?

---

Can the limit ordinal labelled ?? (which seems to be countable) be characterized rigorously (not just by dots) and does it have a name or notation, eventually?

---

[Added] Thanks to Miha's suggestion I learned a little bit about fundamental sequences. So the question is about the limit of the fundamental sequence $\lbrace \omega \uparrow^n \omega\rbrace_{n \in \mathbb{N}}$. Maybe it's enough to characterize this ordinal just like this. But it would be interesting how it could be characterized otherwise.

[Added] Maybe it's trivial, but I had to learn (from here) that the limit ordinal under consideration must be a countable ordinal, because the first uncountable ordinal does'nt have a countable fundamental sequence.

Answer 1

The limit is $φ_ω(0)$, where φ is the Veblen function.

To formally define hyperoperations, you need to define the case $y=0$, and also (for infinite ordinals) the behavior at limit ordinals. I assume reasonable values at $y=0$, and continuous (or otherwise reasonable) behavior at limit $y$.

Your nesting of parentheses is different from the standard treatment of hyperoperations, which is relevant given non-associativity of exponentiation and higher hyperoperations. For example, in your definition, $x↑↑y = x^{x^y}$ (since $(x^x)^x = x^{x^2}$ and so on).

However, $x ↑^{n+1} (y+1) = (x ↑^{n+1} y) ↑^n x = ((x ↑^{n+1} y) ↑^n (x-1)) ↑^{n-1} (x ↑^{n+1} y)$, so while (for finite arguments) your $↑^n$ is slower (for $n>1$) than the standard $↑^n$, your $↑^{2n}$ is still faster than the standard $↑^n$, and your $↑^n$ has the benefit of working well unmodified for infinite arguments.

$x↑↑↑y$ essentially iterates exponentiation, and if $ω≤x<ε_0$, $x↑↑↑(ω+ωy) = ε_y$.
$(ω+x) ↑^{2n+1} (ω+x)$ is probably between $φ_n(x)$ and $φ_{n+1}(x)$.

However, we do not need precise bounds to get the limit point, which is $φ_ω(0)$. If we start with 0 and iterate $φ_n$ $ωα$-times, adding 1 at limits to escape the fix-points, the result will be $φ_{n+1}(α)+1$. The hyperoperations sequence grows at a similar general rate/recurrence, with finite increments of $n$ corresponding to finite increases of $n$ in $φ_n$, so the limit is $φ_ω(0)$.

To go further, you can continue hyperoperations transfinitely (with continuous or otherwise reasonable values at limit $n$). $↑^{2α}$ (with your nesting of parentheses) will roughly correspond to $φ_α$, and the supremum of ordinals expressible this way (allowing hyperoperations inside $α$) is $Γ_0$.

You can also approach $φ_ω(0)$ with appropriately defined one variable functions/hyperoperations. For example, set $f_0(x)=x$, $f_n(0)=1$ ($n>0$), and $f_{n+1}(x+1) = f_n(f_{n+1}(x)⋅2)$ with $f_n(x)$ continuous in both $n$ and $x$. We have $f_ω(x) = φ_ω(0)$ if $ω<x≤φ_ω(0)$; and $Γ_0$ is the least ordinal $α$ such that $f_α(ω+1)=α$.