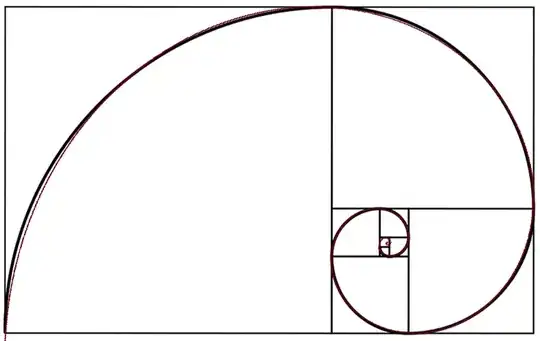
I am trying to create a graphic that shows the golden spiral created using a pentagram and the golden triangles contained therein.
I have drawn out the pentagram and golden triangles and the subsequent smaller triangles and pentagrams that are needed to construct the golden spiral, but when I try to fit the golden spiral onto it, I can't seem to get it to fit.
Is there a difference between the golden spiral created using the golden rectangle method (which is where the formula I used to plot the spiral came from) and the golden spiral created using the golden triangle method? It seems that they should be the same, considering they have both been called a "Golden Spiral"
The equation I am using to plot the spiral (in red on the graphic) is $$r=\phi^{\left(\dfrac{2\theta}{\pi}\right)}$$
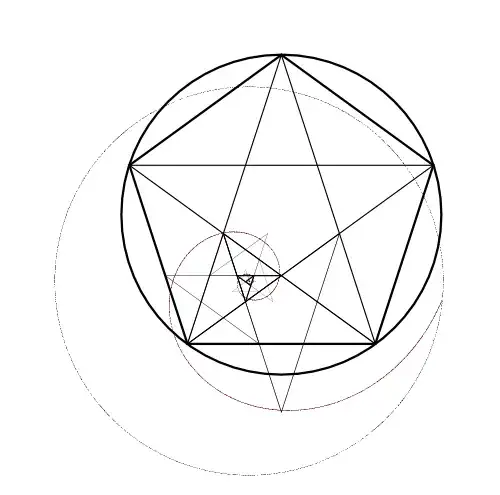
As you can see, the spiral I plotted in Maple does not fit the vertices of the golden triangles as seen on the Golden Triangle Wikipedia page. At points near to the origin of the spiral, the spiral seems to be too tight, but further out, it seems to be too loose.
Any suggestions on the proper formula to use to get a logarithmic spiral that fits?
Is this indeed a golden spiral? Or am I mistaken in believing that the spiral created this way is a golden spiral?
UPDATE: for Ross Millikan
The way I reached the formula I have is through an alternate form for the equation of a logarithmic spiral: $r=ac^{\theta}$ where $c=e^{b}$ and when calculating for the Golden Spiral gives a $c$ value of $c=\phi^{\left(\dfrac{2}{\pi}\right)}$. Substituting this into the original equation and simplifying, gives my original equation for the Golden Spiral.
I have compared the spiral graph generated this way with a Fibonacci Spiral and it matches extremely closely, whereas the spiral generated by the equation in your solution does not match at all, as it is much too wide.
Black is the Fibonacci Spiral, red is my Golden Spiral graph: