-2

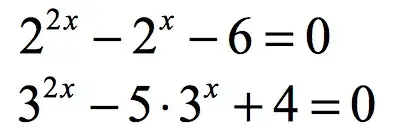
enter image description here

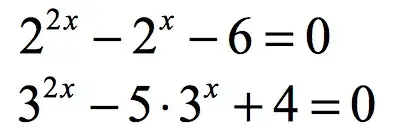
$$2^{2x}-2^x-6=0$$

$$3^{2x}-5\cdot 3^x+4 = 0$$

No clue how to approach this problem..

Martin Sleziak
  • 53,687
Kevin Li
  • 113

3 Answers3

2

Hint:

In each case, you have quadratics in $b^x$:

In the first, put $\;y = 2^x$. Then you have $y^2 - y - 6 = 0$.

For the second, put $\;y = 3^x$. Then you have $y^2 - 5y +4 = 0$.

Note: Both quadratic equations factor quite nicely.

$\begin{align} (1)\quad (2^x)^2 - 2^x - 6 = 0 & \overset{y = 2^x}{\quad \implies\quad} y^2 - y - 6 = (y-3)(y+2) = 0 \\ \\ &\quad\iff y = 2^x = 3 \;\text{ or }\; y = 2^x = -2\end{align}$

We can see immediately that in both solutions, $2^x$ must necessarily be positive, since $2>0$. So we're left with $$2^x = 3 \implies \ln(2^x) = \ln 3 \iff x\ln 2 = \ln 3 \iff x = \dfrac{\ln 3}{\ln 2}\tag{1}$$

$\begin{align} (2)\quad (3^x)^2 - 5(3^x) +4 = 0 & \overset{y = 3^x}{\quad \implies\quad} y^2 - 5y +4 = (y-1)(y-4) = 0 \\ \\ &\quad\iff y = 3^x = 1 \;\text{ or }\; y = 3^x = 4\end{align}$

So we have $$3^x = 1 \implies \ln(3^x) = \ln 1 \iff x\ln 3 = \overbrace{\ln 1 }^{=\,0}= 0 \iff x = 0\tag{1}$$

And we have $$3^x = 4 \implies \ln (3^x) = \overbrace{\ln 4}^{=\ln(2^2) = 2\ln 2} \iff x\ln 3 = 2\ln 2 \iff x = \dfrac {2\ln 2}{\ln 3}\tag{2}$$

amWhy
  • 209,954
  • I'm not sure I understand. What do you do with 2^x if you substitute y for 2x? – Kevin Li Dec 04 '13 at 22:42
  • 1
    you should let lower ranking users answer this kind of question to encourage and motivate them. You are $100k$. You should be answering harder question, and let the easy ones serve as encouragement for new users. – ILoveMath Dec 04 '13 at 22:43
  • @DonAnselmo I'm not here for the rep...I'm here mostly to help the site and to help the users who visit MSE. Have you followed Brian M. Scott? He's in excess of 200K rep, and answers MANY less challenging questions. There's not just the challenge of content to consider; there is also the pedagogical challenge involved. "Being 'good' in math, by itself, does not a good teacher make." – amWhy Dec 04 '13 at 22:44
  • That is strange because I have seen @Brian M. Scott mostly answers topology and hard combinatorics questions. I dont think he answers questions of this level of dificulty. – ILoveMath Dec 04 '13 at 22:56
  • Yes, @Don, many such questions. It's not all he does, just as it's not all I do...but he does. – amWhy Dec 04 '13 at 23:03
  • 1
    @DonAnselmo: Brian M. Scott does answer an occasional easy question or two. I see no problem with this, as this does provide good answers, even for the easier questions. I don't mean to stifle newer users, but it is not pleasant for higher rep users to have to tiptoe around questions which might be seen as too easy. I usually try to avoid easy questions, but once in a while, an easy question can be cathartic, not to mention I think I might be able to give a good answer. – robjohn Dec 10 '13 at 07:59
1

Put $2^{x}=X$ and you have a quadratic equation $X^2-X-6=0$ with solution $X_1=3$ and $X_2=-2$ and finally from $2^{x_k}=X_k$ you have $x_k=\frac{\log X_k}{\log 2}$ for $X_k\ge 0$.

The same for the second equation with $3^{x}=X$.

alexjo
  • 14,976
1

a. Let $2^x = m \implies m^2 - m - 6 = 0$

Solve the quadratic equation to get: $$(m+2)(m-3) = 0 \implies m = -2, \space m =3$$

But remember $2^x = m$ so: $$\therefore 2^x = -2, \space 2^x = 3$$

$\ln$ both sides of the equation to get:

$$\ln 2^x = \ln 3 \implies x\ln 2 = \ln 3 \implies x = \frac{\ln 3}{\ln 2}$$

$$\ln 2^x = \ln - 2$$ You cannot take the $\ln $ of a negative number so that solution is not applicable.

$$\therefore x = \frac{\ln 3}{\ln 2}$$

b. Let $3^x = n \implies n^2 -5n + 4 = 0$

Solve the quadratic equation to get: $$(n-4)(n-1) =0 \implies n = 1, \space n = 4$$

But remember $3^x = n$ so: $$\therefore 3^x = 1, \space 3^x = 4$$

$\ln$ both sides of the equation to get: $$\ln 3^x = \ln 1 \implies x\ln 3 = ln 1$$ but $$\ln 1 = 0 \implies x = 0$$

$$\ln 3^x = \ln 4 \implies x\ln 3 = \ln 4 \implies x = \frac{\ln 4}{\ln 3}$$

$$\therefore x = 0, \space x = \frac{\ln 4}{\ln 3}$$

Zhoe
  • 2,415