I find this picture of the ordinal numbers up to $\omega^\omega$ rather hard to grasp:
I wonder if the following might be a more compelling way to visualize ordinal numbers up to $\omega^\omega$:
My questions are:
(Where) has this way of visualization been suggested before?
How far can it been generalized by repeating the indicated step in a transfinite way?
The "indicated step" is: rotating the picture by 90° counter-clockwise.
The first and second images are essentially the same. They both use a similar system to a logarithmic scale. Imagine the number line but where 0 is you have 1, where 1 is you have 3, at 2 you have 9, and so on. Essentially the further you go along on the scale, the closer the numbers get to each other. Using this principle, you could create a very simple way of expanding these diagrams to include many more ordinals, possibly to the order of ε0 even. If at the place of 0 you had 1, at the place of 1/2 you have 2, at the place of 3/4 you have 3, at the place of 7/8 you have 4, at the place of 1 you would have ω, at the place of 1 + 1/4 you would have ω + 1, so on. With each infinite distance getting infinitely closer each time. I’m assuming the limit of expanding like this would be something much higher that ω^ω, possibly even the Bachman-Howard Ordinal (google it if you really want to know), though going much beyond that would require infinite numbers of infinite recursions and might be hard to depict.
And to answer the first question, I’ve been scourging the internet for any information on this field for 4 years and I haven’t seen that visualisation anywhere before so I would say it hasn’t been done before.
Hopefully you’re still here, and if so thanks for reading this very long winded answer.
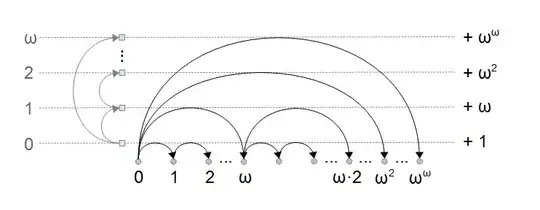
Perhaps this is too trivial of an answer (so let me know if this should be deleted). Here is one way to think about it.
You would definitely be aware of the relation of $\omega^\omega$ with "finite list of natural numbers". Obviously there is nothing special about it in a generic sense (except that the correlation between the two seems easy enough to relate precisely without having to write anything down). Now what I just wanted to point out was that there are two different ways that we can make this association.
$(1)$ A list $(a_n,a_{n-1},...,a_0)$ of length $n+1$ whose first element is non-zero (in other words, $a_n \ne 0$). So, for example, if we had the list $(1,0,2,0,0,3)$ it is supposed correspond to $\omega^5+\omega^3 \cdot 2+3$.
$(2)$ There is another simple way of making an association. Any finite list is supposed to correspond to a unique element now. Informally, we can visualise blocks of $\omega,\omega^2,\omega^3,\omega^4,...$ placed next to each other.
So if we are given something like $(0,6)$, this element must lie in the the second block (the one after $\omega$). So this list is supposed to correspond to $\omega+6$. In general, any $(a,b) \in \mathbb{N}^2$ is supposed to correspond to $\omega+\omega \cdot a+b$.
Similarly, if we had something like $(5,4,3,2)$, then this element must lie in the fourth block (the one after $\omega^3$). This list is supposed to correspond to $\omega^3+\omega^3 \cdot 5+\omega^2 \cdot 4+\omega \cdot 3+2=\omega^3 \cdot 6+\omega^2 \cdot 4+\omega \cdot 3+2$.
For arbitrary list $(a_n,a_{n-1},...,a_0)$ of length $n+1$, we are imagining our element after $\omega^n$ block. So the corrresponding element will be $\omega^n+\omega^{n}\cdot a_n+\omega^{n-1}\cdot a_{n-1}.....+\omega \cdot a_1+a_0$. In particular observe that if we had $(a_n,0,...,0)$, we get $\omega^n+\omega^{n}\cdot a_n$.
Similarly one can imagine a description like $(2)$ (along very similar lines) for $\omega^{\omega \cdot 2}$. We can imagine blocks of $\omega^{\omega+1},\omega^{\omega+2},\omega^{\omega+3},\omega^{\omega+4},....$ placed next to each other.
But this time, we would just require two finite lists. If $x$ was the required element, the first list would pinpoint the unique value $p$ such that $\omega^\omega \cdot p \le x < \omega^\omega \cdot (p+1)$. The second list would pinpoint the unique value $q$ such that $x=\omega^\omega \cdot p + q$.
