$G$ is a group.
If $H, K \le G, |H|, |K| < \infty$, then $$|HK| = \frac{|H||K|}{|H \cap K|}$$
How to prove it?
UPD:
I tried to prove that this function is bijective:
So if i prove it, I can do next thing:
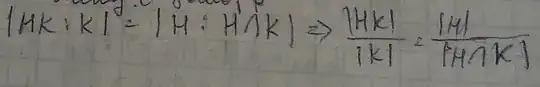
But how to prove it?
Asked
Active
Viewed 395 times
0
michaeluskov
- 73
-
1How did you try to prove it? – Boris Novikov Dec 19 '13 at 16:15
-
Have you studied quotient groups? Do cosets ring a bell? Group theory is an extensive subject. What is the context? What do you know? Depending on the approach of the instructor, there might be an 'obvious' method. – Christopher K Dec 19 '13 at 16:31
-
Look Herstien's Algebra book. I detailed easy proof is given. – Babai Dec 19 '13 at 16:32
-
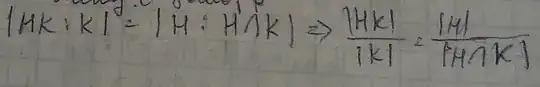
@BorisNovikov I added my thoughts about how to prove it. – michaeluskov Dec 19 '13 at 16:47
1 Answers
1
Hint (1): define a map $\phi: H \times K \rightarrow HK$, by $\phi((h,k))=hk$. Try to show that an element $g \in HK$ has exactly $|H \cap K|$ preimages. (No need to introduce cosets here!)
Hint (2): if $x \in H \cap K$, then $\phi((hx,x^{-1}k))=\phi((h,k))$.
Nicky Hekster
- 49,281