Equation $x^y=y^x\land x\neq y$ has trivial solution $ y(x) = x$. Is there non trivial solution given say in terms of elementary or special functions as $y(x)$? A solution that would yield $y(2) = 4$ and $y(4) = 2$ - among of course all other real numbers $x > 0$.
Asked
Active
Viewed 209 times
5 Answers
3
I already answered this question here in the 3rd comment. If $W(t)$ is Lambert W function, then solution is
$ y(x) = \begin{cases} e^{-W_{-1}\left(-\log \left(x^{\frac{1}{x}}\right)\right)} & 0<x<e \\ e^{-W\left(-\log \left(x^{\frac{1}{x}}\right)\right)} & e<x \end{cases} $
With the graph that looks like (so no trivial $x = y$ part present):
Vitaliy Kaurov
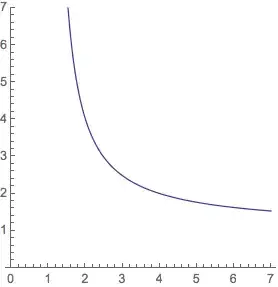
- 196
2
if you take the $xy$-th root of your equation, it yields:
$$x^{\frac1x} = y^{\frac1y} $$
David Holden
- 18,040
-
How does this advance toward an analytic solution? – Alex Wertheim Dec 24 '13 at 21:23
-
2@AWertheim: Now you can solve for $x$ or $y$ in terms of the other using the Lambert W function (nonelementary special function). Rewrite the exponentials in $e^x$ form, take the $\ln$ of both sides and make the appropriate substitution. – The_Sympathizer Dec 24 '13 at 21:25
-
2@mike4ty4 thanks for the elaboration. David, would you mind updating your answer to incorporate some of this information, assuming this is what you had in mind? It's not immediate to me from what you've written alone. – Alex Wertheim Dec 24 '13 at 21:27
-
I think the difficulty lies in specification of domains for various branches, because Lambert W function is multi-valued. The trick I think is to write down carefully some perhaps pieces-wise explicit form with correct domains specifications; - which discards the trivial $x = y$ solution. – iLie Dec 24 '13 at 21:57
1
As far as I remember Lambert's W function can solve some of such equations. If I'm not mistaken, Euler was the first person who studied the solutions of this equation in details and he wrote a treatise on Lambert's W function with his work toward an infinite series that converged to the Lambert W function in a restricted radius. His work possibly motivated Lagrange's inversion formula. I guess nowadays Lambert's W function has been studied well and you might find much more information regarding it.
user66733
- 7,379
1
There are no non-trivial and non-elementary solutions to the functional equation $x^{y(x)} \equiv y(x)^x$.
The so-called Lambert W-function can be used to describe the solution.
Besides the trivial $y=x$ solution, there is also the following:
$$y(x) = -\frac{x\operatorname{LambertW}\left(-\frac{\ln x}{x}\right)}{\ln x}$$
I asked Maple to plot the solutions to $x^y=y^x$ in the range $0 \le x, y \le 10$ and got the plot attached below. The diagonal line is the trivial solution $y=x$. The other is the LambertW solution.
Fly by Night
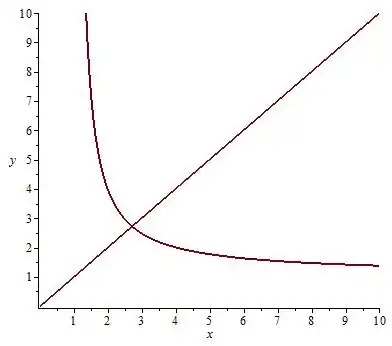
- 32,272
-
If you plot that function you will not get exactly what we need. See this - so you are very close, but the function plots wrong mix of branches. We need I think a proper piece-wise definition do discard $x\neq y$ and another formula to pic up the upper branch. – iLie Dec 24 '13 at 23:13
-
@ILie You asked for a solution with $y$ as a function of $x$. The function I gave satisfies that request. If you allow $x$ to be a function of $y$ then you get a similar solution with $x$ and $y$ interchanged. Combining these two charts gives us the complete picture (which I also supplied). – Fly by Night Dec 25 '13 at 00:03
-
Your function has a part where x = y, which is against of one of the stated conditions. See attached image in my previous comment. – iLie Dec 25 '13 at 00:23
-
@ILie the image you attached also includes the line $x=y$ for small $x$. Your attached image is a proper subset of mine. Just as $y=\sqrt{x}$ is a proper subset of $y=x^{1/2}$. – Fly by Night Dec 25 '13 at 01:08
1
The function $f(x)=x^{1/x}$ is strictly increasing, in $(0,\mathrm{e})$, as
$$
f'(x)=x^{1/x}\left(\frac{1-\ln x}{x^2}\right)>0,
$$
and strictly decreasing in $(\mathrm{e},\infty)$, with
$$
\lim_{x\to 0}x^{1/x}=0 \quad \text{and} \quad \lim_{x\to\infty}x^{1/x}=1.
$$
In particular, every value in the interval $(1,\mathrm{e}^{1/\mathrm{e}})$ is taken twice by $f$, i.e., for all $a\in(1,\mathrm{e}^{1/\mathrm{e}})$, there exist $x,y$, such that
$$
1<x<\mathrm{e}<y \quad\text{and}\quad x^{1/x}=y^{1/y},
$$
and thus $x^y=y^x$. Let's see now how can we express $y=y(x)$. Let $f(x)=x^{1/x}$, where $x\in(1,\mathrm{e})$. Then, the unique $y\in(\mathrm{e},\infty)$, with the property that $f(x)=f(y)$ is equal to:
$$
y=\left(\left(\,f\restriction_{(\mathrm{e},\infty)} \right)^{-1}\circ f\right)(x).
$$
The function:
$$
g=\left(\,f\restriction_{(\mathrm{e},\infty)} \right)^{-1}\circ f :(1,\mathrm{e})\to (\mathrm{e},\infty),
$$
is clearly 1-1 and onto, strictly decreasing, and $C^\infty$, and satisfies
$$
x^{g(x)}=\big(g(x)\big)^x \quad\text{and}\quad x<\mathrm{e}<g(x).
$$
Yiorgos S. Smyrlis
- 83,933