In diamond $ABCD$,such $\angle B=\dfrac{\pi}{3}$,and the point $E$ in on $BC$.such $BE=3CE$,and the point $F$ is on $DE$,such $\angle AFC=\dfrac{2\pi}{3}$
Find $$DF=?$$
My try: since $$\angle B+\angle AFC=\pi$$ so $A,B,C,F$ is cyclic
and follow I can't
First some experiment with Cinderella to see what the result should be.
Here Cinderella computed the distance ratio numerically, then its guess function tried to turn that number into a likely algebraic expression. Usually this works well, particularly for small constructions with nice numbers like this one here. The third line is only for myself to check that I made no obvious error in rewriting that algebraic term.
So now you know that the correct result should be $DF=\sqrt{\frac37}AB$.
You can proove this using explicit coordinates for all points.
\begin{align*} A &= (1,0) & D &= (0,0) \\ B &= \left(\frac32,\frac{\sqrt3}2\right) & C &= \left(\frac12,\frac{\sqrt3}2\right) \\ E &= \left(\frac34,\frac{\sqrt3}2\right) & F &= \left(\frac37,\frac{2\sqrt3}7\right) \end{align*}
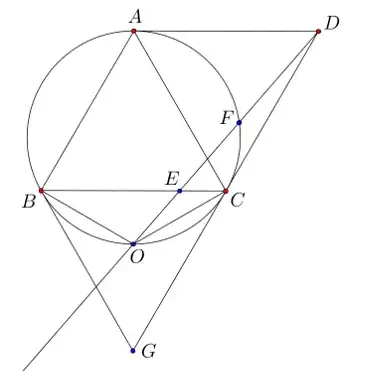
The coordinate system was chosen to make things easier. Point $F$ was computed using the guess from above, namely using $\overrightarrow{DF}=\sqrt{\frac37}\frac{\overrightarrow{DE}}{\left\lVert\overrightarrow{DE}\right\rVert}$. Now all that remains to show is that $A,B,C,F$ are cocircular.
$$ \begin{vmatrix} x_A^2+y_A^2 & x_A & y_A & 1 \\ x_B^2+y_B^2 & x_B & y_B & 1 \\ x_C^2+y_C^2 & x_C & y_C & 1 \\ x_F^2+y_F^2 & x_F & y_F & 1 \end{vmatrix} = \begin{vmatrix} 1 & 1 & 0 & 1 \\ 3 & \frac32 & \frac{\sqrt3}2 & 1 \\ 1 & \frac12 & \frac{\sqrt3}2 & 1 \\ \frac37 & \frac37 & \frac{2\sqrt3}7 & 1 \end{vmatrix} = 0 $$
So the point $F$ with the distance $DF$ as guessed above is indeed cocircular as you found it must be, so it is the right point.
Without Cinderella, you would not have the coordinates of $F$ up front, so you could assume $\overrightarrow{DF}=\lambda\,\overrightarrow{DE}$ for some $0<\lambda<1$, then write your cocircularity test as
$$ \begin{vmatrix} 1 & 1 & 0 & 1 \\ 3 & \frac32 & \frac{\sqrt3}2 & 1 \\ 1 & \frac12 & \frac{\sqrt3}2 & 1 \\ \frac{21}{16}\lambda^2 & \frac34\lambda & \frac{\sqrt3}2\lambda & 1 \end{vmatrix} = -\frac{21\sqrt3}{32}\lambda^2 + \frac{5\sqrt3}4\lambda - \frac{\sqrt3}2 = 0 $$
Since you only test whether the result is zero or not, you may simplify things by scaling rows or columns by some non-zero factor, so you might prefer to actually compute something like
$$ \begin{vmatrix} 1 & 4 & 0 & 1 \\ 3 & 6 & 1 & 1 \\ 1 & 2 & 1 & 1 \\ \frac{21}{16}\lambda^2 & 3\,\lambda & \lambda & 1 \end{vmatrix} = -\frac{21}{4}\lambda^2 + 10\,\lambda - 4 = 0 $$
Whether you simplify or not, the solutions you end up with will be
$$ \lambda_1 = \frac47 \qquad \lambda_2 = \frac43 > 1 \\ DF=\lambda_1\,DE = \frac47 DE = \frac47\sqrt{\frac9{16}+\frac34} AB =\sqrt{\frac37} AB $$
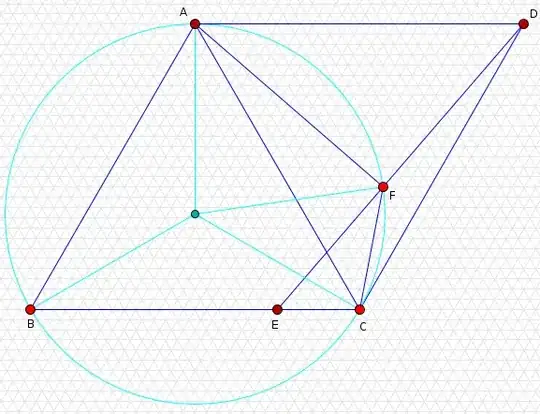
@DonAntonio wrote in several comments that he'd prefer a geometric solution. I have no ready solution yet, but this rational $DF=\frac47DE$ looks like it might stand a chance of being useful. Playing around with the configuration, I also noticed that $\angle DFA=\frac\pi2$, although I have neither proof for this nor a clear idea of how it might be useful. Nevertheless, here is another picture to illustrate both these facts:
Let's draw another equilateral triangle $BCG.$ Let $O$ be the center of that triangle.
Let's show that points $D, E$ and $O$ are collinear $\Longleftrightarrow$ points $D, F$ and $O$ are collinear.
$\overrightarrow{DE}=\overrightarrow{DC}+\overrightarrow{CE}=\overrightarrow{DC}+\dfrac{1}{4}\overrightarrow{CB},$
$\overrightarrow{DO}=\dfrac{1}{3}\left(\overrightarrow{DB}+\overrightarrow{DC}+\overrightarrow{DG}\right) = \dfrac{1}{3}\left(\overrightarrow{DA}+\overrightarrow{AB}+\overrightarrow{DC}+2\overrightarrow{DC}\right)=\dfrac{1}{3}\left(\overrightarrow{CB}+4\overrightarrow{DC}\right) = \dfrac{4}{3}\overrightarrow{DE}.$ Thus, $D, F, E$ and $O$ are collinear.
Since $\angle COB + \angle BAC = \dfrac{2\pi}{3} + \dfrac{\pi}{3} = \pi,$ all five points $B, A, F, C$ and $O$ are concyclic.
The circumscribed circle of $\triangle ABC$ is tangent to line $DC$, which follows from the fact that $\angle BAC = \dfrac{\pi}{3} = \angle BCG.$ As an alternative, it can be observed from the symmetry of the picture with respect to the perpendicular bisector of $AB.$
It follows from the tangent-secant theorem that $DC^2 = DF\cdot DO.$ We know $DC,$ we want $DF,$ so the only thing that's left to calculate is $DO.$
We use cosine formula for that. Assuming the side of any of the equilateral triangles is $a$, $DO^2 = CD^2+CO^2-2\cdot CD \cdot CO \cos \cfrac{5\pi}{6}=a^2+\dfrac{a^2}{3} + 2a\dfrac{a}{\sqrt{3}}\dfrac{\sqrt{3}}{2} = \dfrac{7}{3}a^2.$
So $DF = a^2\bigg/\sqrt{\dfrac{7}{3}a^2}=\sqrt{\dfrac{3}{7}}a = \sqrt{\dfrac{3}{7}}AB$
You can draw your whole figure onto a triangular grid. The trick here is getting it rotated correctly, namely in such a way that the line $FA$ aligns with one of the grid lines. Then $FC$ will be a grid line as well if you place $F$ at a grid line crossing. Scale everything untill all the points end up on intersections of grid lines, and you obtain something like this:
Then you can check that all the angles and distance ratios match your description simply by looking at the grid displacements. I've also drawn in the circumcircle for $ABCF$, but you don't need that since $\angle AFC=\frac23\pi$ is readily apparent.
I found this by noticing that $\angle BFE=\angle EFC=30°$. I wanted to orient things in such a way that this fact was more readily apparent, so I drew $FE$ vertical and $FC$, $FB$ as rays $30°$ on either side. I then intersected $FC$ with a vertical line one step left of $F$, and $FB$ with one three steps right, to obtain $C$ and $B$ such that $CE:BE=1:3$ as required. Since that $E$ turned out to not be on a grid line intersection, I doubled the grid density, and got the result above.
What you can read off this result is the fact $DF=\frac47DE$, as I already saw in my other answer. Relating it to those other lengths, particularly to the edge lengths $AB=AC=BC=AD=CD$, would introduce square roots, but even that would be possible to compute from that grid and the coordinates it suggests.
If you know what you're after, you could do the same thing in an unrotated version, but in that case the grid would have to be much finer to place all points on grid line intersections:
This fine grid makes the counting a lot harder, so the statement is more difficult to verify here. And the circumcircle radius to $F$ now looks completely different from the other three, while in the image above it was only reflected.
