2

Hopefully this kind of question is ok, have seen a couple of other WA-queries that hasn't been downvoted. Apologies if not.

I'm trying to find the max/min of a complex function over certain domains, the unit disk or circle for example. It doesn't seem as though Wolfram Alpha understands what I'm trying to say though.

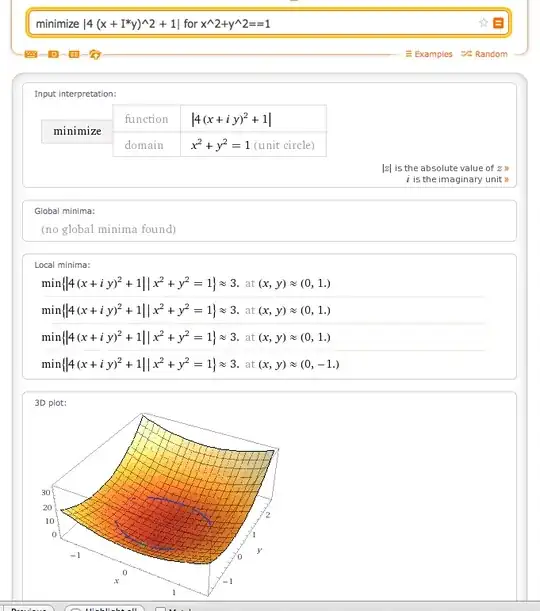
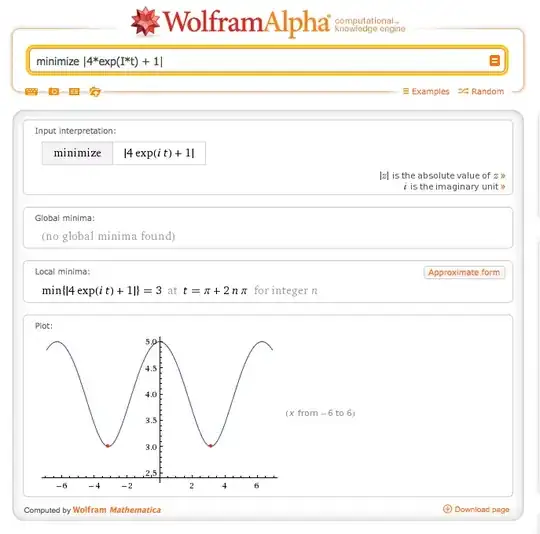
For example if I try $4z^2 +1, |z|=1$, WA just ignores the absolute value restriction. I've tried mod(z), abs(z), $\{|z|=1\}$ and some other stuff. Documentation only seems to contain examples over the reals. Any guesses?

Benjamin Lindqvist
  • 3,112
  • 1
    "min 4z^2+1 with |z|=1" seems to work – zarathustra Jan 05 '14 at 08:44
  • If $z \in \mathbb C$, then what does it mean to ask for the "maximum" of $4z^2 + 1$? $\mathbb C$ is not an ordered field. – heropup Jan 05 '14 at 08:49
  • Good point but I think it's clearly implied that it's the maximum of the modulus we're looking for. Antoine's suggestion worked fine! Although strictly speaking, I guess min |4z^2 +1| with |z|=1 would be more correct. – Benjamin Lindqvist Jan 05 '14 at 08:58
  • "min |4z^2+1| with |z|=1" indicates that the minimum is 5, yet $|4i^2+1|=3$, which is less than 5. Thus, it seems that WA is assuming the input is real. – Mark McClure Jan 05 '14 at 14:38

1 Answers1

2

Optimization problems generally assume real input an output. Accordingly, WolframAlpha assumes this type of input. You can get around this issue by recasting your problem in terms of real real variables. For example:

minimize |4 (x + I*y)^2 + 1| for x^2+y^2==1

enter image description here

or

minimize |4*exp(I*t) + 1|

enter image description here

Mark McClure
  • 30,510