Difference between one to one function and one to one correspondence

Question

I am confused in the difference between one to one function and one to one correspondence. Please help me out to distinguish between the two. Thanks

Answer 1

a one to one function can be injective or bijective but a one to one correspondence can only be bijective

Answer 2

Hope this helps you understand things a bit better. I too had the same question a while ago...

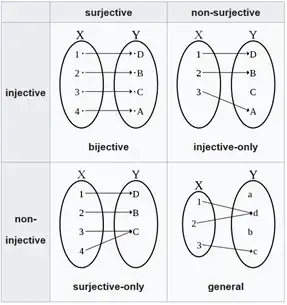
Types of Mappings/Functions

a. Injective mapping (injection): one-to-one mapping = is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain.

b. Surjection: onto mapping = a function f from a set X to a set Y is surjective (or onto), or a surjection, if for every element y in the codomain Y of f there is at least one element x in the domain X of f such that f(x) = y. It is not required that x be unique; the function f may map one or more elements of X to the same element of Y.

c. Bijective mapping (bijection): one-to-one and onto mapping = one-to-one correspondence

[NOTE: bijectivity (one-to-one correspondence) is a necessary condition for functions to have inverses, whereas injectivity (one-to-one mapping) solely will not help in guaranteeing inverses].

Answer 3

1. one to one means injective (a mapping $f$ which maps distinct elements of its domain to distinct elements of its codomain, i.e. $f(x) \neq f(y)$ whenever $x \neq y$ )
2. one to one correspondence means bijective (a mapping $f$ which is injective AND for every element $y$ in the codomain of $f$, there exists an element of $x$ in the domain of $f$ such that $f(x) = y$ )

Answer 4

I would say (hand waveingly) a one to one function is a mapping from A to B that puts A & B into one-to-one correspondence with each other, for one to one and function as defined in your previous questions.