4

Find the equilibrium solutions of the following differential equation:

$$\dfrac{dy}{dt} = \dfrac{(t^2 - 1)(y^2 - 2)}{(y^2 -4)}$$

I'm not sure how to go about doing this since t appears explicitly on the right hand side. Would $y = \sqrt{2}$ or $-\sqrt{2}$ be solutions?

user51462
  • 673
  • 6
  • 12
  • 31

2 Answers2

10

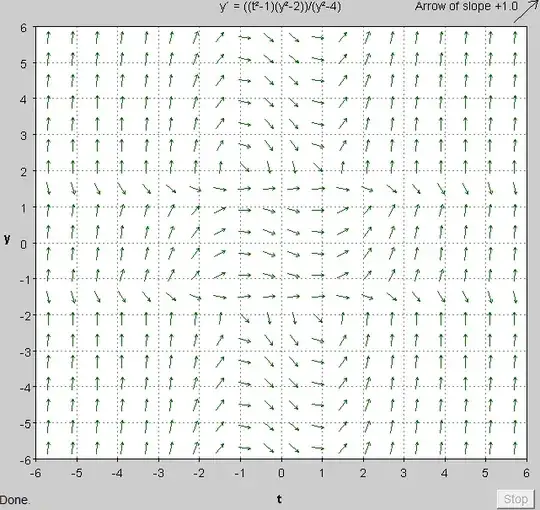
We are looking for where the derivative $\dfrac{dy}{dt} = 0$.

This is satisfied when $y^2-2 = 0$ and you do not want $y^2 - 4 = 0$ (division by zero).

This leads to the two equilibrium points, $y = \pm \sqrt{2}$.

We can find a closed-form solution (ugly) for this DEQ:

$$y(t)-\dfrac{\ln(\sqrt{2}-y(t))}{\sqrt{2}}+\dfrac{\ln(y(t)+\sqrt{2})}{\sqrt{2}} = c+\dfrac{t^3}{3}-t$$

A direction field plot shows (look at $y = \pm~ \sqrt{2}$):

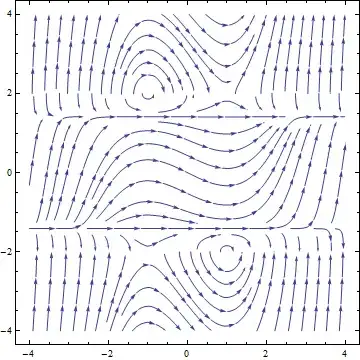
enter image description here

Additionally, if we look at $t = \pm 1$, on the following direction field plot, we can see the horizontal tangents as:

enter image description here

Amzoti
  • 56,093
  • 1
    It should also be mentioned that all the "flow curves" have horizontal tangents at "times" $ \ t \ = \ \pm 1 \ $ ; this is the contribution of the $ \ t^2 - 1 \ $ factor in the differential equation. – colormegone Jan 17 '14 at 04:36
  • There is a slightly less "ugly" form of the solution of the DEQ. It is

    y + Sqrt(2) ArcTanh[y / Sqrt(2)] = t^3 /3 - t + Cte

    Given the constant, the equation is quite easy to solve for a given value of "t" or a given value of "y".

     – Claude Leibovici Jan 17 '14 at 05:45
  • @Amzoti Thank you. I still can't make sense of the $t^2−1$ factor on the right hand side. Is this an example of a nonautonomous DEQ? There is no mention of nonautonomous equations in the chapter the question pertains to so I tried searching for similar questions online but to no avail. – user51462 Jan 19 '14 at 08:01
0

I think your equilibrium solutions are $y=\pm \sqrt2$ if by equilibrium it is meant $\frac{dy}{dt}=0$, i.e. steady-state.

Paul Safier
  • 661