10

Can you please answer this question with explanation ? I just learned about the charts needed to cover 1 and 2 spheres but got confused for the case of torus. It would be great if you guys could help.

Mush
  • 103

4 Answers4

17

If the images of the charts are not restricted to be simply connected (which they are not according to the Wikipedia definition of "chart"), then there is a two-chart-system covering the torus.

$\qquad\qquad\qquad\qquad\quad\quad$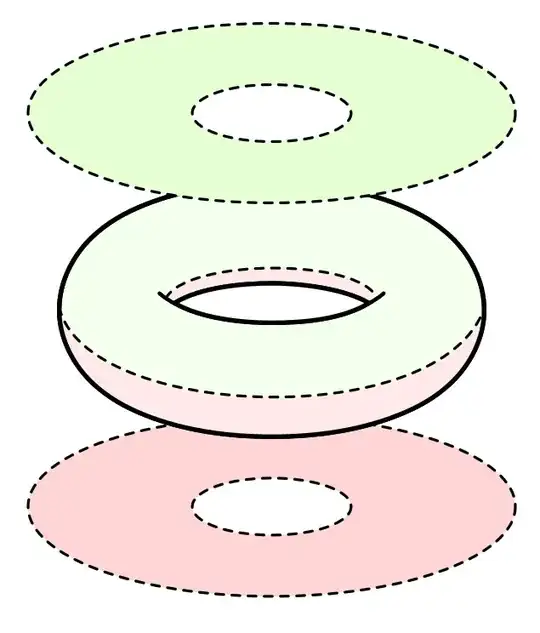

And even with simply connected open sets, there is a way to do it with only three charts. Here is a picture showing how these charts look like on the flat torus (the right one shows that they indeed cover everything).

enter image description here

M. Winter
  • 29,928
  • I know this is an old post, but just a follow-up comment/question. For the non-simply connected images, wouldn't we need two more charts to cover the outer and inner rings at the discontinuity between the upper and the lower patches (along the dotted lines in the image you provided)? – metsburg Jul 01 '23 at 10:32
  • 1
    @metsburg The image is not perfect in retrospect. Just imagine the regions to extend a bit more up and down respectively, so that they overlap in an annulus. – M. Winter Jul 02 '23 at 09:01
  • Thanks, that makes perfect sense. – metsburg Jul 03 '23 at 12:29
6

Hint $\mathbb T^2=\mathbb S^1\times\mathbb S^1$

It is easily to see that $\mathbb S^1$ can be charted by two covers, then $\mathbb T^2$ is four.

gaoxinge
  • 4,434
5

Four will do it. Wrap one around the outside of the doughnut and another on the inside. Let them overlap a little. Both of these are diffeomorphic to hollow cylinders, which require two patches to cover.

ncmathsadist
  • 49,383
  • 2
    I know this is an old answer, but I have a question. Do you assume that the images of your charts $\phi:U\to \Bbb R^2$ are simply connected? As far as I can tell (e.g. from the definition from Wikipedia), this is no part of the definition of chart. Because if you do not assume this, then the cylinders are diffeomorphic to annuli in $\Bbb R^2$ and these two maps suffice to cover the torus. – M. Winter May 04 '18 at 12:33
  • @M.Winter This deserves a seperate answer. Please turn your comment into an answer so I can upvote it. – Babelfish Aug 28 '18 at 16:28
  • @Babelfish Thanks for motivating me to answer. I added one below. – M. Winter Aug 29 '18 at 08:42
1

You need a minimum of 3 (contractible) charts. Denote by T your 2-torus. First you can cut along a set A of "figure 8" of the torus so that T\A is a topological disk/square and T\A is your 1st chart. The figure 8 is a very small set inside T, so you can cut out another set B of “figure 8” such that T\B is also a topological disk/square such that A intersect B consists of two points and T\B is your 2nd chart. Finally, you need a 3rd chart of disk to cover the two points.

This is a special case of Lusternik–Schnirelmann category. In general, under some mild conditions, you can usually cover an n-dimensional manifold with (n+1)-charts.

By the way, how do I do LaTeX here?

Eugene Z. Xia
  • 111
  • 1
    You use MathJax (see here), almost the same as TeX. BTW, in your question you should have said that your charts are contractible, which is not a universal convention. – Moishe Kohan Feb 15 '22 at 04:45