1

I have two questions.

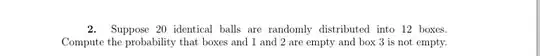
(1) enter image description here

solution(1): Sample size $=|S|=12^{20}$

$11^{20}\rightarrow$ guarantee that one box is empty.

$10^{20}\rightarrow$ guarantee that two boxes are empty.

$9^{20}\rightarrow$ guarantee that three boxes are empty.

Then, $$P=\frac{10^{20}-9^{20}}{12^{20}}$$

(2) a box contains 12pairs of shoes. If 8 shoes are rondomly selected, what is the probabilty that there willie exactly one complete pair?

Answer: $$\frac{12\binom{11}{6} 2^6}{\binom{20}{8}}$$

I solved first question. But I am not sure the solution. Please check it. And I cannot understand the second question's answer. How is the answer written? Please explain it step by step. Thank you:)

1190
  • 6,458
  • 4
  • 43
  • 97

2 Answers2

1

I think the answer to the first one is $\binom{28}{9}/\binom{31}{11}$.
Reason:
This is a partition problem since the balls are identical. Partitioning 20 identical balls among 10 boxes can be done in $\binom{29}{9}$. But we put one ball in the 3rd (fixed) box. And we are only left with 19 balls to be distributed among 10 boxes(boxes 3-12). Hence $\binom{28}{9}$.

Number of ways of distributing n identical objects among r groups

Community
  • 1
Swapniel
  • 540
  • This assumes that all partitions are equally likely. It is possible to make that assumption. However, that is not the appropriate model for applications such as hashing. A partition with the first box getting all the balls is then far less probable than a partition with a fairly even distribution. – André Nicolas Feb 27 '14 at 14:51
0

There are $\binom{24}{8}$ equally likely ways to choose $8$ shoes.

Let us count the number of ways to have exactly one pair. The "type" of shoe we have two of can be chosen in $\binom{12}{1}$ ways. That leaves $6$ non-matching shoes to be chosen.

The types of shoe we have $1$ each of can be chosen in $\binom{11}{6}$ ways. And for every collection of $6$ types, we can choose the left shoe or the right shoe of each type, for a total of $2^6$. Thus the number of "favourables" is $\binom{12}{1}\binom{11}{6}2^6$.

The first answer is correct.

André Nicolas
  • 507,029
  • That is, $\binom{20}{8}$ is false. The true one is $\binom{24}{8}$. Right? – 1190 Feb 26 '14 at 20:02
  • Yes, that is written in the answer. I did not comment on it because it looked like an obvious typo. – André Nicolas Feb 26 '14 at 20:04
  • 1
    Your solution to the first problem is wrong. – Swapniel Feb 27 '14 at 02:39
  • I did not write out a solution to the ball problem. OP's answer is correct. The natural model is that we throw balls toward the boxes one at a time, with all boxes equally likely. Imagine the balls to be distinct, it makes no difference to the probability. Then there are $12^{20}$ equally likely outcomes. Let $A$ be the event first two boxes are empty, and $B$ the event first three are empty. There are $10^{20}$ outcomes in $A$. We must subtract the $9^{20}$ outcomes in $B$, giving a total of $10^{20}-9^{20}$ favourable outcomes. – André Nicolas Feb 27 '14 at 02:50
  • 1
    It does make difference. However let us consider the balls are distinct. Then the answer should have been $10^{19}/12^{20}$. See my post before I edited it. – Swapniel Feb 27 '14 at 09:19
  • Distinctness of balls is, to repeat, not relevant. What matters is the model we use. The model with $10^{20}$ equally likely outcomes comes from assuming that the destinations of the balls are chosen independently, with all destinations equally likely. – André Nicolas Feb 27 '14 at 14:45
  • http://math.stackexchange.com/questions/47345/number-of-ways-of-distributing-n-identical-objects-among-r-groups Still if you don't get that having identical objects matter, I have nothing else to say.. – Swapniel Mar 01 '14 at 16:09