What is this shape called?
Asked
Active
Viewed 788 times
3
-
8It probably doesn't have a specific name. – Ragib Zaman Oct 06 '11 at 09:17
-
1I too doubt that it is named, but $1+b+c+\frac{b \log (b)}{\log (2)}+\frac{c \log (c)}{\log (2)}+(1-b-c) (\log (1-b-c)+\log (\log (2)))=0$ looks to be a simpler form. How did you come across this oval? – J. M. ain't a mathematician Oct 06 '11 at 09:41
-
6It is called an egg. – I. J. Kennedy Mar 04 '12 at 15:18
1 Answers
4
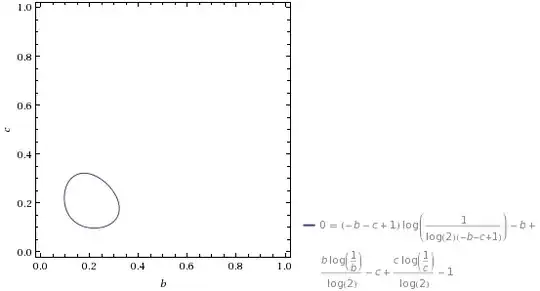
This would not fit in the comments
I think you may have made an error in your legend: by symmetry it is more likely to be something like $$(1-b-c)\log\left(\frac{1}{1-b-c}\right)/\log(2) + b\log\left(\frac{1}{b}\right)/\log(2) + c\log\left(\frac{1}{c}\right)/\log(2) - b - c - 1 = 0.$$
If so, this would be easier to read as $$(1-b-c)^{1-b-c} b^b c^c 2^{b+c+1} = 1$$ though that seems to have the real solution $b=c=1/4$ rather than your curve, so perhaps it should be something different.
Perhaps you could tell us the origin of your curve and the expression
Henry
- 157,058